




Next: About this document ...
Up: REFERENCES
Previous: Solving for the extrapolation
The expression for 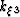 forms the basis for a one-way extrapolation operator that can be used to propagate wavefields on generalized coordinate meshes. This requires that a wavefield at step
forms the basis for a one-way extrapolation operator that can be used to propagate wavefields on generalized coordinate meshes. This requires that a wavefield at step 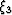 (i.e.,
(i.e., 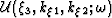 ) be propagated to the next step
) be propagated to the next step 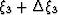 (i.e.,
(i.e., 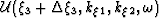 ) according to
) according to
| 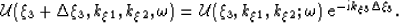 |
(32) |
The back-projection of residuals required for waveform inversion can be implemented easily according to the adjoint process of equation 32,
| 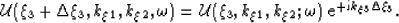 |
(33) |
Note that the coefficients above are spatially variant which requires employing a typical approach (e.g. split-step Fourier, FFD or phase-screens) for developing a mixed 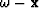 domain exponential operators. This study uses the split-step Fourier approach detailed in Shragge (2006a) using the extrapolation wavenumber
domain exponential operators. This study uses the split-step Fourier approach detailed in Shragge (2006a) using the extrapolation wavenumber 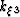 defined by equation 31.
defined by equation 31.





Next: About this document ...
Up: REFERENCES
Previous: Solving for the extrapolation
Stanford Exploration Project
1/16/2007