




Next: Algorithm for Computation
Up: Shragge: Differential gridding methods
Previous: Acknowledgements
- Alkhalifah, T., 2003, Tau migration and velocity analysis: Theory and synthetic examples: Geophysics, 68, 1331-1339.
-
- Guggenheimer, H., 1977, Differential Geometry: Dover Publications, Inc., New York.
-
- Liseikin, V., 2004, A Computational Differential Geometry Approach to Grid Generation: Springer-Verlag, Berlin.
-
- Rüger, A. and D. Hale, 2006, Meshing for velocity modeling and ray tracing in complex velocity fields: Geophysics, 71, U1-U11.
-
- Sava, P. and S. Fomel, 2001, 3-D traveltime computation using Huygens wavefront tracing: Geophysics, 66, 883-889.
-
- Sava, P. and S. Fomel, 2005, Riemannian wavefield extrapolation: Geophysics, 70, T45-T56.
-
- Shragge, J. and P. Sava, 2005, Wave-equation migration from topography: 75st Ann. Internat. Mtg., SEG Technical Program Expanded Abstracts, 1842-1845.
-
- Shragge, J., 2006, Generalized riemannian wavefield extrapolation: SEP-124.
-
A
This appendix details a numerical scheme for solving the differential
gridding equations discussed in Liseikin (2004). The set of
parabolic equations to solve are,
| ![\begin{eqnarray}
\frac{ \partial s^1}{ \partial t} = D^{\xi}[s^1] + D^{\xi}[f^k]...
...1,\xi^2), & t=0 \
s^2(\xi^1,\xi^2,0) = s^2_0(\xi^1,\xi^2), & t=0\end{eqnarray}](img45.gif) |
(19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
where,
| ![\begin{eqnarray}
D^{\xi}[v] = & g_{22}^{\xi} \frac{\partial^2 v}{\partial \xi^1
...
...}(\mathbf{\xi})] }{\partial \xi^j},
\quad i,j,k=1,2, \quad m=1,l.\end{eqnarray}](img38.gif) |
(25) |
| (26) |
Computational domain 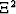 is the unit square divided into N
intervals equally spaced in the
is the unit square divided into N
intervals equally spaced in the 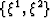 directions. The
first transformation
directions. The
first transformation 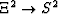 interrelates the known
coordinate values on boundaries of domains S2 and
interrelates the known
coordinate values on boundaries of domains S2 and 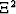 ,
,
| ![\begin{displaymath}
\Phi (\xi^j) = \left[\phi^1 (\xi^j),\phi^2 (\xi^j) \right], \quad j=1,2. \end{displaymath}](img47.gif) |
(27) |
The interior points of S2 are generated using blending functions,
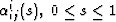 , where
, where 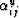 is linear
function defined by,
is linear
function defined by,
| 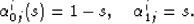 |
(28) |
Blended coordinates 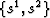 are generated on S2 with,
are generated on S2 with,
| ![\begin{eqnarray}
s^{1}(\xi^{1},\xi^{2},0) = F^{1}(\xi^{1},\xi^{2})+(1-\xi^{2})
\...
...ight]+
\xi^{2} \left[\phi^{i}(\xi^{1},1)-F^{2}(\xi^{1},1) \right],\end{eqnarray}](img51.gif) |
|
| (29) |
where,
| 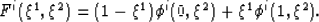 |
(30) |
Equations 1924 can be solved using
finite difference approximations that march forward in time. To
simplify notation coordinates s1 and s2 are redefined as u=s1
and v=s2. The
finite difference solution is split into a two-stage process along the
different coordinate axes. The first stage calculates solutions
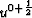 and
and 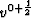 for a step in the u
direction at time
for a step in the u
direction at time 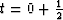 using the values u0 and
v0. The second stage calculates solutions u0+1 and v0+1
for a step in the v direction at time t=0+1 using intermediate
values
using the values u0 and
v0. The second stage calculates solutions u0+1 and v0+1
for a step in the v direction at time t=0+1 using intermediate
values 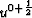 and
and 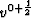 .
.
Explicitly, the four equations comprising the finite difference scheme
for unij and vnij, 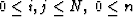 on uniform grid
on uniform grid
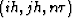 are,
are,
| 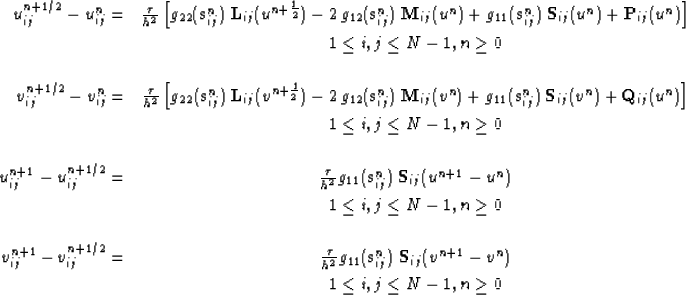 |
|
| (31) |
| |
| |
| (32) |
| |
| |
| (33) |
| |
| |
| (34) |
where,
| ![\begin{eqnarray}
g_{11} \left(\mathbf{s}^n_{ij}\right)= &
\left(\frac{ u^n_{i+1...
...right]& \nonumber \
\;& k=1,l \quad \; \quad 1\le i,j \le N-1 &\end{eqnarray}](img59.gif) |
|
| (35) |
| |
| |
| |
| (36) |
| |
| |
| |
| (37) |
| |
| (38) |
| |
| (39) |
| |
| (40) |
| |
| (41) |
| |
| |
| (42) |
![\begin{eqnarray}
\frac{ \partial s^1}{ \partial t} = D^{\xi}[s^1] + D^{\xi}[f^k]...
...1,\xi^2), & t=0 \
s^2(\xi^1,\xi^2,0) = s^2_0(\xi^1,\xi^2), & t=0\end{eqnarray}](img45.gif)
![\begin{eqnarray}
\frac{ \partial s^1}{ \partial t} = D^{\xi}[s^1] + D^{\xi}[f^k]...
...1,\xi^2), & t=0 \
s^2(\xi^1,\xi^2,0) = s^2_0(\xi^1,\xi^2), & t=0\end{eqnarray}](img45.gif)
![\begin{eqnarray}
D^{\xi}[v] = & g_{22}^{\xi} \frac{\partial^2 v}{\partial \xi^1
...
...}(\mathbf{\xi})] }{\partial \xi^j},
\quad i,j,k=1,2, \quad m=1,l.\end{eqnarray}](img38.gif)
![\begin{eqnarray}
s^{1}(\xi^{1},\xi^{2},0) = F^{1}(\xi^{1},\xi^{2})+(1-\xi^{2})
\...
...ight]+
\xi^{2} \left[\phi^{i}(\xi^{1},1)-F^{2}(\xi^{1},1) \right],\end{eqnarray}](img51.gif)
![]() and
and ![]() for a step in the u
direction at time
for a step in the u
direction at time ![]() using the values u0 and
v0. The second stage calculates solutions u0+1 and v0+1
for a step in the v direction at time t=0+1 using intermediate
values
using the values u0 and
v0. The second stage calculates solutions u0+1 and v0+1
for a step in the v direction at time t=0+1 using intermediate
values ![]() and
and ![]() .
.![]() on uniform grid
on uniform grid
![]() are,
are,
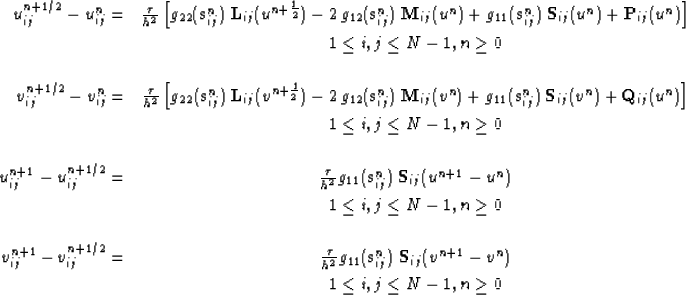
![\begin{eqnarray}
g_{11} \left(\mathbf{s}^n_{ij}\right)= &
\left(\frac{ u^n_{i+1...
...right]& \nonumber \
\;& k=1,l \quad \; \quad 1\le i,j \le N-1 &\end{eqnarray}](img59.gif)