Operator

Theoretical considerations or problem descriptions often represent linear transformations by matrices. In scientific and engineering applications, as in the convolution example above, these matrices are often large and sparse. An implementation of such a transformation as an explicit matrix multiplication is inefficient. Instead Jest utilizes the more general concept of operator interfaces and leaves implementation details to each application. The operator concept, of course, includes the specific implementation of a linear operator as a matrix but also generalizes to nonlinear transformations.

 

$$y \leftarrow f(x)$$ image y = f.image(x)

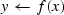$$y \leftarrow f(x)$$ image f.image(x,y)

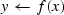$$y \leftarrow y + f(x)$$ addImage f.addImage(x,y)

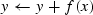getDomain f.getDomain() returns vector space

 

The convolution ${\bf B}$ in our example is a linear operator that implements Jest's operator interface. A few operator methods are listed in Table 4. The interface for a linear operator with adjoint is called hasAdjoint and extends the operator interface by a method adjoint() that returns the adjoint operator of the original operator. Many solvers require a linear operator's adjoint. The deconvolution example uses a simple convolution class Tcai and its adjoint; both implement the hasAdjoint interface. An auxiliary class TcaiFactory creates the needed transient convolution object.