 |
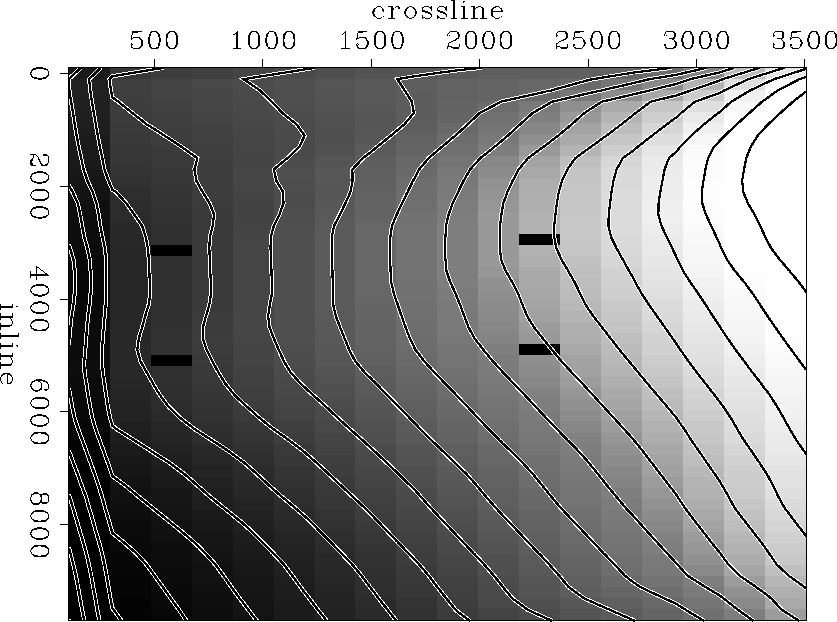
Figure 1 Synthetic seismic data comprising 18 lines of 50 data points each. The four well locations are indicated with black rectangles.
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
ABSTRACTWell log information and seismic data for a given horizon may not tie properly. I address the problem by formulating a least-square inverse problem for a synthetic dataset. The aim of my regression equations is to find a model with a regular grid by simultaneously linear interpolating the well data and mapping the trend of the seismic information. I have scaled the second regression equation to decrease the dominance of the seismic over the well data. First I determine a prediction-error filter (PEF) from the seismic data and then run a conjugate gradient solver with the PEF to create the final map of the horizon. With this new method, the final map matches the wells more accurately. |
INTRODUCTION
Geophysicists obtain the location of horizons in depth by various ways. Analysis of well data produces information precise enough to give an accurate depth position for geological horizons. The time position of an interface depends on many parameters and processing steps, which endangers its accuracy. Therefore the seismic data is less accurate than the well data. Ultimately, I want to reconcile these two kinds of data taking into account their differences in accuracy.
In his book Three-Dimensional Filtering (TDF), Jon Claerbout proposes that a least-square inversion scheme can solve the problem of well data not matching seismic data.
I have tested the scheme with different parameters on a 2-D synthetic model. This paper presents the results of my investigations. First, I formulate the problem as described in TDF; then I modify the theory proposed by Claerbout, to find a solution that works best for the given synthetic data.
THE PROBLEM OF TYING WELL TO SEISMIC DATA
Geophysicists are interested in knowing as precisely as possible the location in depth of geologic horizons to determine where to drill. Commonly a field survey is composed of several seismic lines shot on the prospect and usually several wells drilled to gain knowledge about the lithology and physical parameters of the rocks (velocity, density, and so on.) During a survey, many seismic lines are shot, whereas only a few wells are drilled because of the high cost of drilling but also because of uncertainty about where to install the next drilling platform.
The new drilling sites are usually chosen on the basis of the processed seismic data. Paradoxically, the information provided by the seismic lines is less accurate than that provided by well data, mainly because of all the steps necessary to process the seismic data. Some of these steps use parameters determined by the person in charge of the processing, which introduces human error. Furthermore, if the seismic data are given in time, they need to be converted in depth using a velocity model so that they can be compared to the well information.
Therefore, it seems more accurate to base the choice of the next drilling site mainly on the reliable information provided by the already existing wells, while taking into account the trend of the seismic data. However, in complex regions or because of the multiple processing steps, the seismic data do not correspond to well data. This article proposes a way to properly tie well information and seismic data, using a synthetic example.
Figure seismic represents the synthetic model I have built to test the algorithm. It comprises four well locations (black rectangles on the figure) and 18 seismic lines of 50 data points each. The contour lines show the trend of the seismic data. The error between the depth at the well and the depth at the same location on the seismic map is between five and ten percent.
 |
A LEAST-SQUARE INVERSION SCHEME
In Three-Dimensional Filtering (TDF), Claerbout describes a way to solve the lack of correspondence between well and seismic data. He proposes the following regression equations for his least-square inversion scheme:
| |
(1) |
| |
(2) |
where w is the well data vector, s represents the seismic data, and m is the model obtained after several iterations of conjugate gradients.
Equation (1) maps the well data onto the model space using linear interpolation, while equation (2) tends to smooth the discrepancy between the seismic data and the model. In equation (2), Claerbout proposes using the Laplacian operator as a roughening filter A.
Figure lap-1000 shows the results after 1000 iterations of conjugate gradients with the Laplacian filter. The surface presents a bell shape around the well locations where the algorithm tried to get the model to match the depth of the wells. The final map looks smooth but does not correctly follow the seismic data (partially because of the bell shaped local surfaces around the wells) and does not seem to take the well information into account sufficiently. Furthermore, I realised that the value on the map at the well location corresponds to a bigger offset from the depth at the well than on the seismic map before any iteration of conjugate gradients.
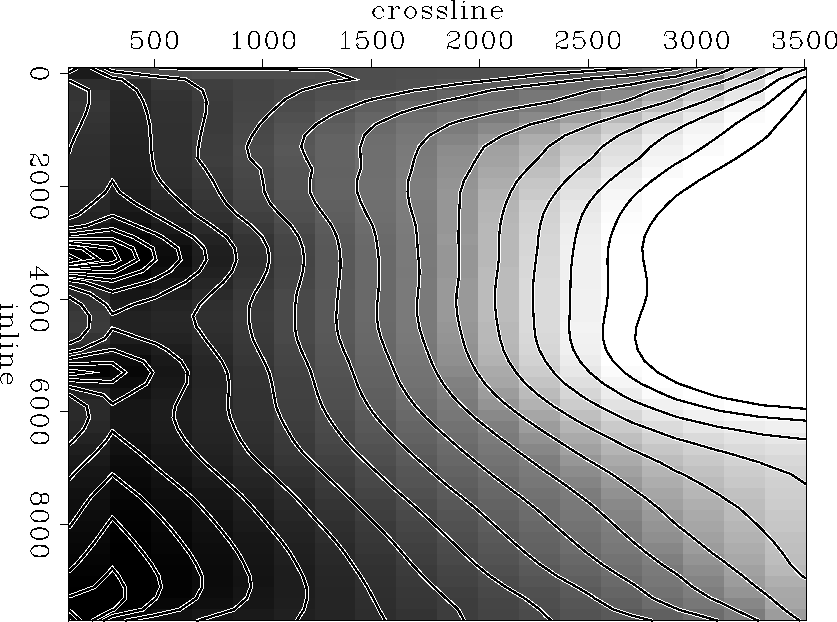 |
These initial results have driven me to change the algorithm in two major ways. First, I need to increase the importance of the well data relative to that of the seismic information. Second, having decreased the importance of the seismic data, I need a better way to get my model to follow the trend of the seismic information.
IMPROVEMENTS ON THE SCHEME
The model map needs to fit the well information as closely as possible. With many more seismic data points than well locations, I need to increase the importance of the well information so that it is quantitatively at least as important as the seismic data.
To do so, I introduce a scaling factor ![]() into equation
(2) of the inversion scheme, as follows:
into equation
(2) of the inversion scheme, as follows:
| (3) |
I have 900 seismic data points and only four well locations. If I choose for
![]() a value equal to 4/900 = 0.0044, the well information and
the seismic data play an equal role in the final model map. For the synthetic
example I have set
a value equal to 4/900 = 0.0044, the well information and
the seismic data play an equal role in the final model map. For the synthetic
example I have set ![]() = 0.001. If
= 0.001. If ![]() gets too small,
then the inversion scheme no longer takes the seismic data into account;
instead it produces big spikes corresponding to the well locations.
gets too small,
then the inversion scheme no longer takes the seismic data into account;
instead it produces big spikes corresponding to the well locations.
The goal is to construct a model map that follows the trend of the seismic information. With the improved version of the algorithm, I first map the seismic data onto the model space by linear interpolation, then determine a prediction-error filter (PEF) from it to predict the trend of the seismic information. The regression equations corresponding to the new scheme are almost identical to the previous ones:
| |
(4) |
| |
(5) |
where ![]() is the seismic data mapped onto the model
space, and
is the seismic data mapped onto the model
space, and ![]() is the scaling factor.
is the scaling factor.
Figure pef-1000 shows the result after 1000 iterations of conjugate
gradients with a PEF of 3 by 3 coefficients and ![]() = 0.001. The
final map follows the trend of the seismic data quite accurately while the
well information, if not fully reflected, is taken into consideration. As a
matter of fact, the map matches the depth of the two wells on the right side
of the figure while it gets close to the correct depth for the two wells on
the left side (the original distance between the seismic data and the depth
at the wells has been divided by a factor of three). Since the synthetic data
are quite predictable and smooth, I did not have to modify the shape of the
PEF to try and get a better result. In the case of a more complex seismic
dataset, the use of patching may become necessary to find several PEFs in
regions with little change of character in the seismic data.
= 0.001. The
final map follows the trend of the seismic data quite accurately while the
well information, if not fully reflected, is taken into consideration. As a
matter of fact, the map matches the depth of the two wells on the right side
of the figure while it gets close to the correct depth for the two wells on
the left side (the original distance between the seismic data and the depth
at the wells has been divided by a factor of three). Since the synthetic data
are quite predictable and smooth, I did not have to modify the shape of the
PEF to try and get a better result. In the case of a more complex seismic
dataset, the use of patching may become necessary to find several PEFs in
regions with little change of character in the seismic data.
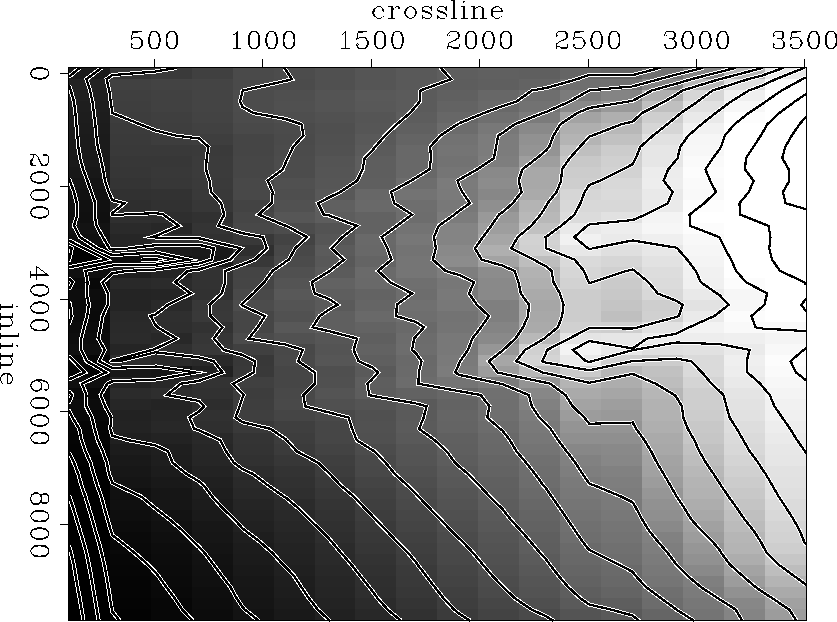 |
The final map after 1000 iterations of conjugate gradients shows two V-shaped ``valleys'' linking the two upper wells on one side and the two lower wells on the other. In Figure pef-1000 these valleys appear as lines almost parallel to the crossline axis connecting the wells. They get shallower close to the well on the right side of the figure. The first regression equation of the inversion scheme, equation (4), creates this feature. Equation (4) indicates that the model should fit the wells as best as possible. Equation (5) indicates that it should also respect the topography of the seismic data. If equation (5) were not included in the inversion scheme, the final map would probably look like a planar surface going through the four well locations. The valleys that appear in Figure pef-1000 are what remains of the surface when the model follows the trend of the seismic data.
CONCLUSIONS
This paper presents a least-square inversion scheme to tie well information with seismic data. With this method, I first determine a prediction-error filter to predict the trend of the seismic information in order to create a final map that reflects the shape of the seismic data. I also introduce a scaling factor to increase the importance of the well in relation to the seismic data. This scheme has produced good results with a synthetic example and now needs to be tested on a real data case.
ACKNOWLEDGMENTS
I would like to thank Sean Crawley and Bob Clapp for the discussions we had together, which helped me understand the flaws in my first approach.
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)