LEAST-SQUARES KIRCHHOFF MIGRATION

To do least-squares Kirchhoff migration, we either have to work in the time domain, as is done by Ji elsewhere in this report, or use time-invariant transforms, despite their apparent inappropriateness.

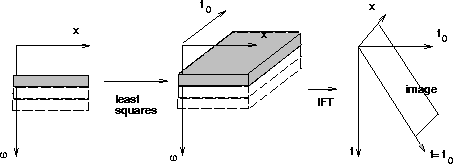
A Kirchhoff migration analog to least-squares slant stacking is summarized in Figure . Since we are using time-invariant transforms, a separate least-squares problem is set up for each frequency. In the slant stack case, this problem involved transformation to a one-dimensional space (ray parameter p), since only one parameter is needed to describe a linear moveout trajectory, its slope.

In the migration case, two parameters are needed to describe a migration hyperbola: the position beneath which the apex of the hyperbola lies (x), and another parameter that describes the curvature of the hyperbola. If we fix velocity, this second parameter can be called t₀. For a given constant velocity, the hyperbola will have greater curvature for an early t₀, and less for a later one. The transform space, then, contains two parameters (x and t₀) instead of one in the slant stack case.

This means that the least-squares problem is likely to be larger than in the slant-stack case, and is typically underdetermined. But in principle there is nothing wrong with the transform space having an extra dimension.

 

mig
Figure 2 Overview of least-squares migration. An underdetermined problem is solved for each frequency to find sources, as a function of x, the position of the hyperbola apex, and t0, the curvature. The image is contained in a single plane of the inverse Fourier transformed cube, but other planes contain information about focusing at other velocities.