The conventional slant-stack transform
takes us from the recorded data d(x,t) to the slant
stack domain ![]() :
:
| L d = m. | (1) |
In the frequency domain, a separate system of equations can be constructed for each frequency. The matrix L contains time shifts, expressed as complex exponentials:
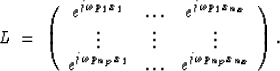 |
(2) |
The conjugate operator LH brings us back to time and space:
| LH m = d. | (3) |
The conjugate operator is the more straightforward of the
two. If we have a point in ![]() space, the operator
LH does a good job of turning it into a line in (x,t)
space, regardless of the number of traces in x; there
is no aperture effect. The forward transform, however, is
affected by the aperture. If we transform a single dipping
event in (x,t) to
space, the operator
LH does a good job of turning it into a line in (x,t)
space, regardless of the number of traces in x; there
is no aperture effect. The forward transform, however, is
affected by the aperture. If we transform a single dipping
event in (x,t) to ![]() there will be artifacts and
a loss of resolution, caused by the limited aperture.
there will be artifacts and
a loss of resolution, caused by the limited aperture.
We would do better to transform from (x,t) to ![]() using the inverse of the matrix LH:
using the inverse of the matrix LH:
| m = (LH)-1 d. | (4) |
However, the matrix LH is typically not square; the problem is either overdetermined or underdetermined. In this case, we can find the best least-squares solution by multiplying both sides of the conjugate transform by L:
| L LH m = L d, | (5) |
giving:
| m = ( L LH )-1 L d. | (6) |
The matrix ( L LH )-1 L is the least-squares inverse of LH.
The least-squares slant stack is summarized in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
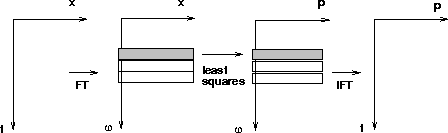 |