RESPONSE OF THE EARTH TO GRAVITATIONAL WAVES

Following Schutz(1988), the response of two masses connected by a spring to a gravitational wave with amplitude h^tt_xx,00 is controlled by

$$\xi_{,00} + 2 \gamma \xi_{,0} + \omega_{0} \xi = \frac{1}{2} l_{0} h^{tt}_{xx,00}$$ (5)

where $\xi$ is the displacement, $\gamma$ is the damping factor, $\omega_{0}$is the resonance frequency, and l₀ is the length of the spring. $\xi_{,00}$ is the second derivative with respect to time, and $\xi_{,0}$ is the first derivative with respect to time. h^tt_xx,00 is the amplitude of the wave as referred to by Schutz(1988).

The solution to this equation when $h^{tt}_{xx,00} = A \cos\Omega t$is

$$\xi = R \cos ( \Omega t - \phi )$$ (6)

where

$$R = \frac{ \frac{1}{2} l_{0} \Omega^2 A}{\sqrt{(\omega_{0}-\Omega)^2 + 4 \Omega^2 \gamma^2}}$$ (7)

and

$$\tan \phi = \frac{2 \gamma \Omega}{\omega_{0}^2 - \Omega^2}$$ (8)

$\Omega$ is the wave's frequency.

If $\omega_{0}^2 - \Omega^2$ is large with respect to $2 \gamma \Omega$, $\phi$ will approach zero and $\xi$ will be proportional to h^tt_xx.

I make a crude assumption that a column in the earth will react like a spring. Away from resonance, the response of the earth to a gravitational wave will be proportional to the strain $\cos(2 \phi) \sin^2(\theta)\cos \Omega t$,where $\phi$ is colatitude and $\theta$ is longitude as given by Hellings (1992). This strain on a sphere for t=0 is shown at an exaggerated scale in Figure  .

 

GWresp2 Figure 5 An exaggerated view of the strain on the earth caused by a gravitational wave. The function plotted is $(\cos(2 \phi) \sin^2(\theta))+2$.

If this response is close to the correct response, the strain of the earth recorded by the IDA network can be predicted. Figure shows the response of the earth as it would appear to the available stations to a source at position 43 of the grid in Figure , using these approximations.

 

daysrc43 Figure 6 The response of the IDA stations to a gravitational wave source at position 43 of the grid in Figure 11. Each trace corresponds to a station in the IDA array.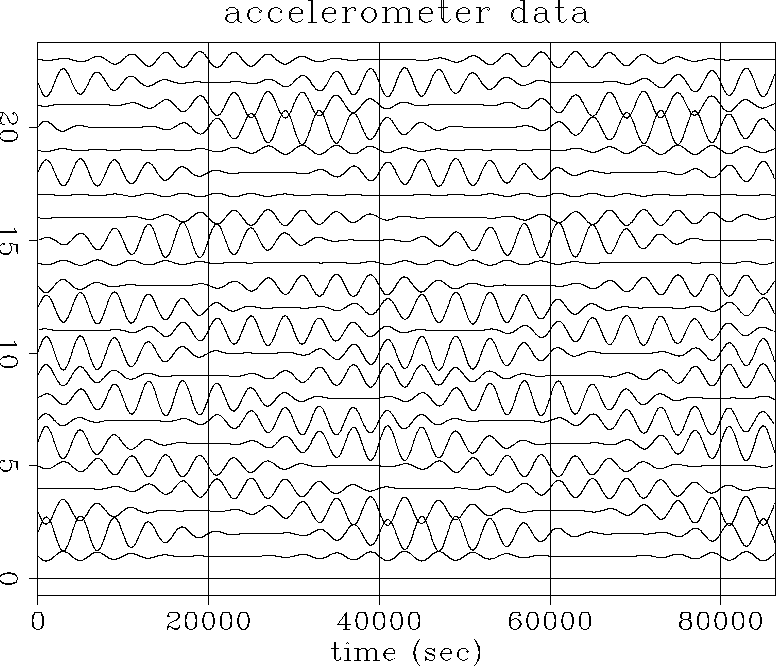