A smooth v(x,z) background velocity model

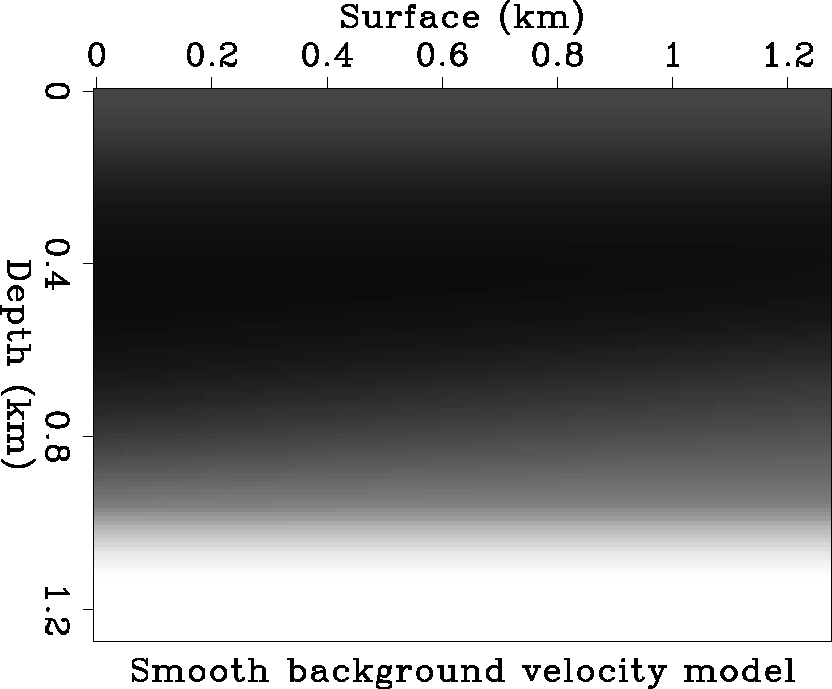
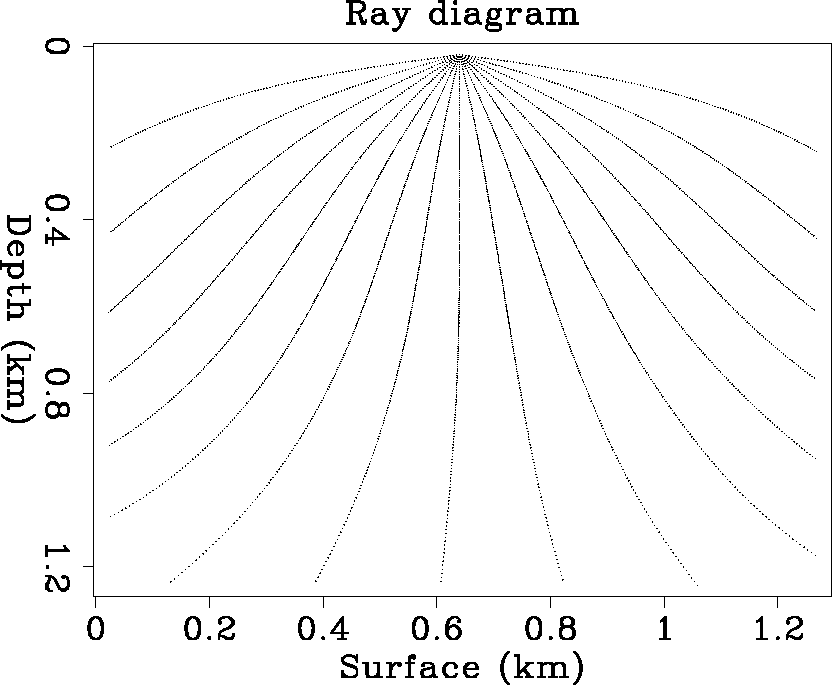
Figure 5 shows a smooth background velocity model. Figure 6 is the ray diagram of 17 rays traced down from one surface location by the Runge-Kutta method. The takeoff angles of the 17 rays are equally spaced from -80 to 80 degrees. As the rays are traced in constant increments of traveltime, the spatial distance traversed per step is longer in high velocity zones (long wavelength zones) than in low velocity zones (short wavelength zones), as can be seen from the different spacing between dots along rays. Ray tracing is stopped when the tangent of the ray is close to horizontal. The ray paths correctly follow the background velocity model. 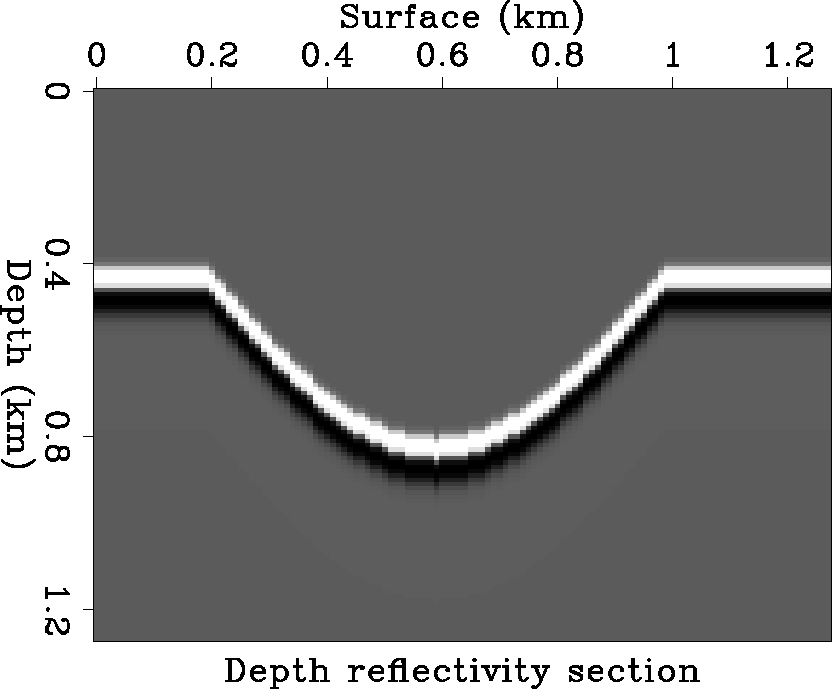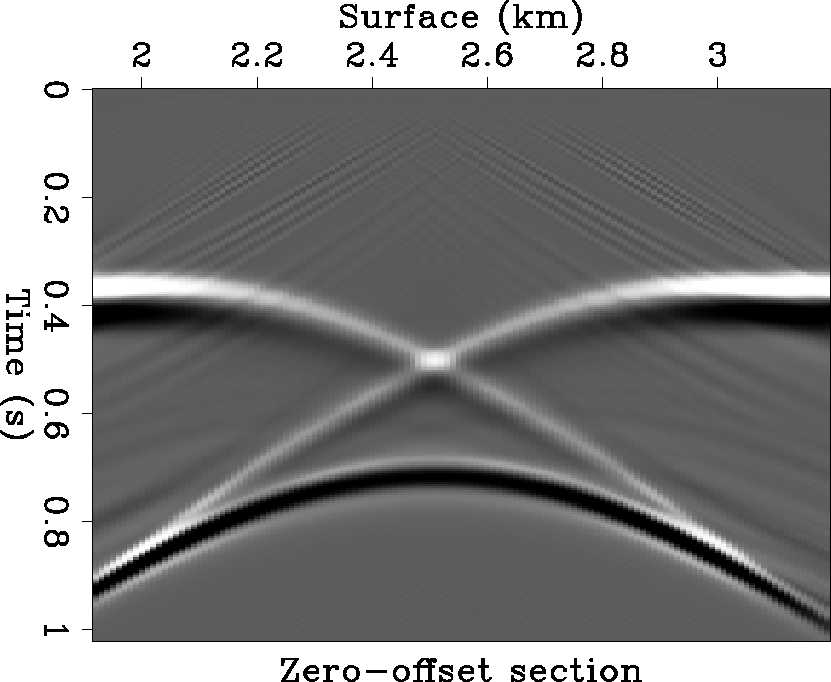Figure 7 is the reflectivity model, with dips ranging from to 45-degree. Figure 8 is the zero-offset section generated by reverse-time migration (Baysal et al., 1983) running in the modeling mode. There is some noise around 0.2 second, generated from the sharp corners of the reflectivity model. 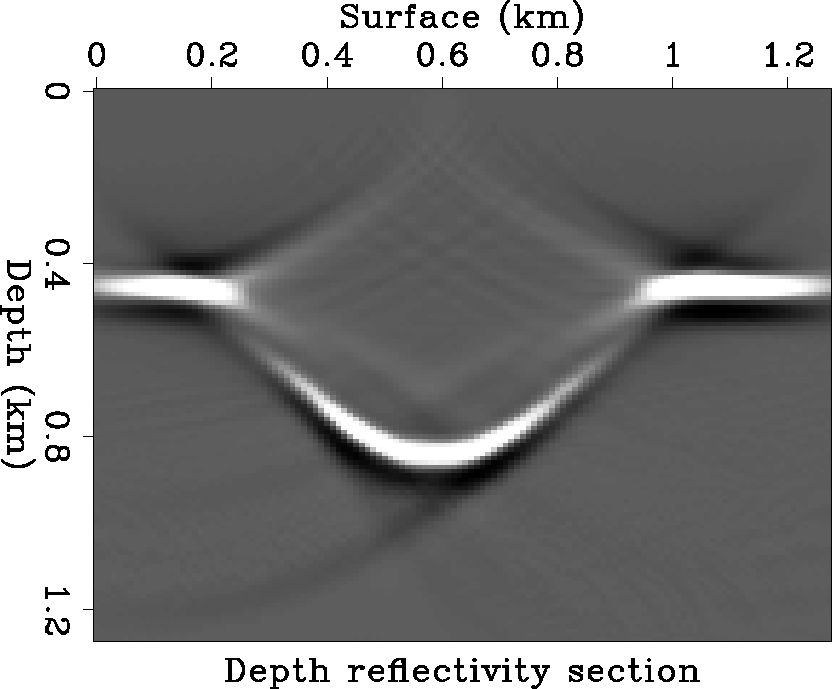Figure 9 is the reflectivity depth image reconstructed by Gaussian beam migration based on ray frames. From each surface source point, 17 rays are traced with takeoff angles equally spaced from -80 to 80 degrees, as in Figure 6. The reconstructed image correctly matches the original reflectivity depth model, and the image background is very clean.

 

Vel.H
Figure 5 Smooth background velocity model.

 

Ray.H
Figure 6 Ray diagrams of 17 rays traced from one surface location through the smooth background velocity model shown in Figure 5.

 

Ref.H
Figure 7 Subsurface depth reflectivity in the smooth background velocity model of Figure 5.

 

Section.H
Figure 8 Surface zero-offset section generated by modeling the subsurface depth reflectivity model in the smooth background velocity model with the reverse-time migration method (Baysal et al, 1983).

 

ImageGB.H
Figure 9 Subsurface depth reflectivity image reconstructed by Gaussian beam depth migration.