The elements of Gaussian beam migration

To demonstrate the basic elements of Gaussian beam migration and migration in general, I have generated a synthetic section (Figure 1) that contains only one nonzero trace and only one isolated wavelet. The maximum time of the section is 0.512. And the migration is to be done in a model with a constant velocity v=1. Thus the maximum possible depth the section can image is 0.512. In this case, I perform the migration in a depth model with a maximum depth of 1, and use only the vertical ray path from the source. The depth image is shown in Figure 2. The Gaussian beams along one ray path can image the neighborhood of the ray path. The figure also explains the dephasing of migration imaging. The depth difference between the two images is 0.512, thus the phase difference of $2 \pi$. The first image appears when the entire upward modeling propagation phase has been exhausted by the Gaussian beam downward propagation, and the second image appears when another propagation phase of $-2 \pi$ has accumulated. The same phenomenon can easily happen in phase shift and finite difference $\omega-x$ depth migration. The figure also demonstrates that as the Gaussian beam propagates, its parabolic wavefront spreads.

 

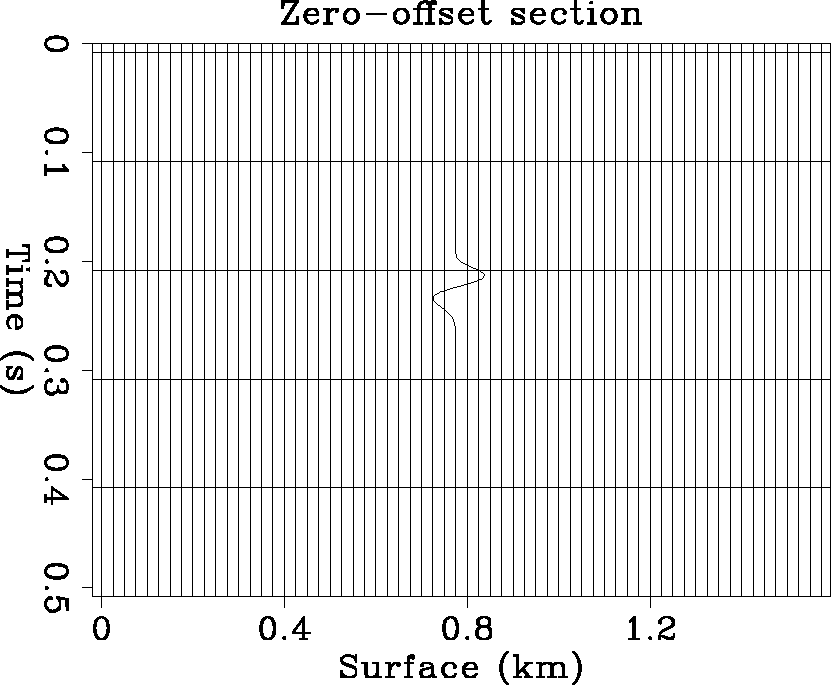Wavelet.H Figure 1 A record section with only one isolated wavelet.

 

DePhase.H Figure 2 Migration is the process of dephasing. The Gaussian beams along one ray path can image the neighborhood. And as the Gaussian beam propagates, its parabolic wavefront spreads.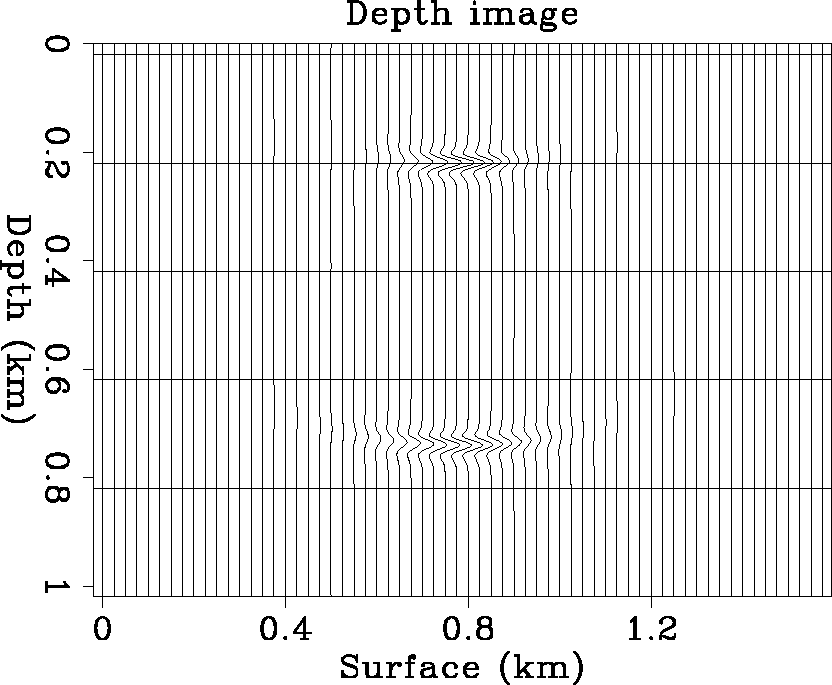

The way to avoid image reappearance is to pad with zeros at the end of the data section, and compute the depth image only to the maximum possible depth. Figure 3 is the depth image generated by migrating the above section with Gaussian beams evaluated along 51 rays from the source, equally spaced from -85 to 85 degrees. For comparison, Figure 4 displays the depth image generated by phase shift migration. In it, Stew Levin's ideas regarding how to avoid wraparound artifacts have been implemented (Levin, 1983; Claerbout, 1985). Here, because the constant velocity v=1, the output of time migration is a depth image. Kinematically, the Gaussian beam migration response correctly matches that of phase shift. However, there is some waveform distortion at high angles. The waveform distortion will be eliminated by careful coordinate interpolation of image points during construction of the Gaussian beams. An advantage of the Gaussian beam migration image over that obtained by the phase shift method is that the image background is much cleaner with Gaussian beam migration.

 

MigGB.H Figure 3 In a constant velocity background model, the migration response of one isolated wavelet is a half circle. This image is produced by Gaussian beam depth migration.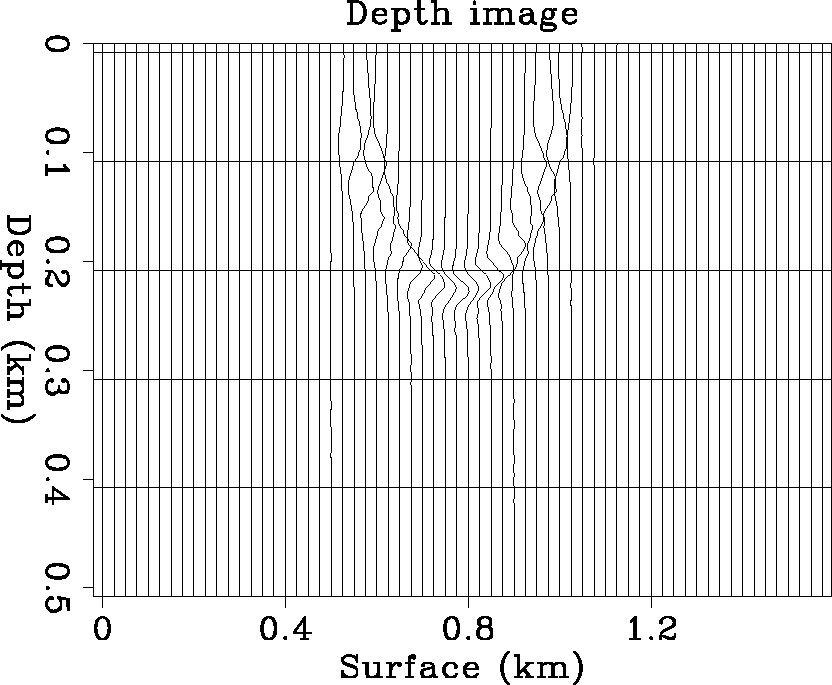

 

MigPhase.H Figure 4 In a constant velocity background model, the migration response of one isolated wavelet is a half circle. This image is produced by phase shift migration.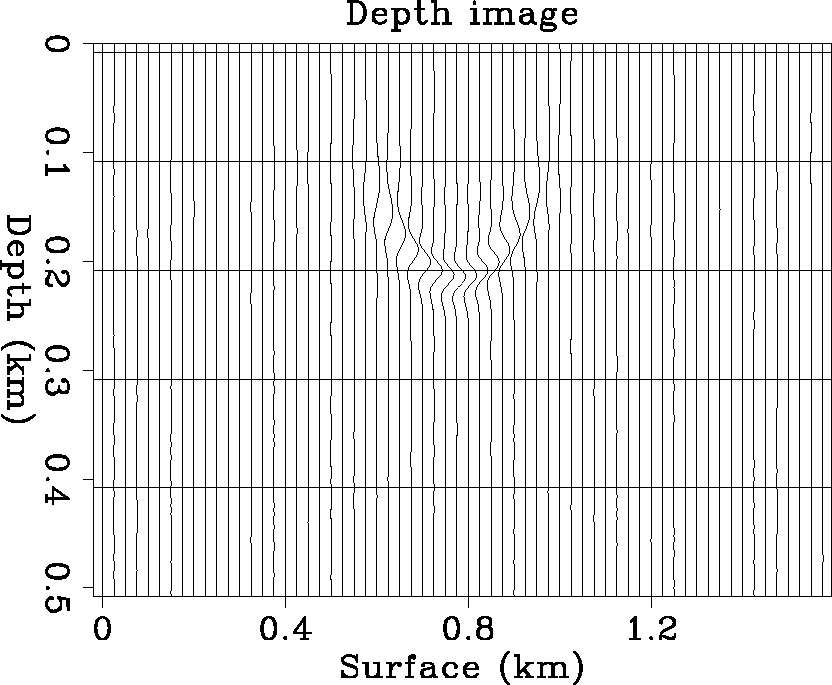