The lowpass filter coefficients

In the section ``Wavelet transform of a vector'' I assumed the matrix C to be orthogonal. Additionally, I stated lowpass and highpass characteristics of the filter coefficients c_k. In this chapter I will derive the simple nonlinear equations for c_k which guarantee these conditions.

To be orthogonal the matrix C in equation (1) multiplied by its transpose in equation (2) has to yield a unit matrix. The multiplication provides the following orthogonality relation for the wavelet filter coefficients c_k:

 

c₀² + c₁² + c₂² + c₃² = 2

 

c₀ c₂ + c₁ c₃ = 0

To determine the four coefficients, two additional relations are required. The conditions

 

c₀ - c₁ + c₂ - c₃ = 0

 

0 c₀ - 1 c₁ + 2 c₂ - 3 c₃ = 0

ensure that any inner product of (c₀,-c₁,c₂,-c₃) and a series k₁ (1,1,1,1) + k₂ (1,2,3,4) yields . This annihilation is called an ``approximation condition of polynomial order 1'' or ``the vanishing of the zeroth and first momentum.'' It is important to note that these rejected polynomials are the low-order and therefore smooth polynomials. These local rejections justify the imaginative visualisation of the odd row multiplications as local highpass filtering. The even row multiplication destroys high-frequency events by weighted adding.

I have coded the conditions in a mathematica script coef.ma, which solves numerically for the coefficient set c_k.

(* coef.ma *)
(* number of coefficients *)
(* tested for n=4 and n=6 *)
n  = 4 ; 
nh = n / 2 ;
(* definitions kronecker & Power *)
kron[i_,j_] := If[ i == j, 1, 0] ;
Unprotect[Power] ;
Power[0,0] = 1 ;
Protect[Power] ;
(* approximation condition *)
Do[aus[i] = Sum[(-1)^k (n-k)^(i-1) c[k], {k,1,n}] == 0, {i,1,nh}]
(* orthogonality condition *)
Do[aus[i+nh] = Sum[ c[k] c[k-2(i-1)] , {k,2(i-1)+1,n}] ==  kron[i,1], {i,1,nh}]
(* solving Equation *)
eqsys = Table[aus[i],{i,1,n}] ;
coef = Table[c[i],{i,1,n}] ;
sol = N[Solve[eqsys,coef]] ;
(* use NSolve[] for numerical results *)
sol >>> sol.ma ;

The conditions (4), (5), (6), and (7) determine the coefficients c_k's amplitude but not their phase spectrum. Daubechies defines her wavelets as the minimum phase solution to these equations. The 4-point wavelet coefficients are  

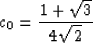$$c_0 = {1 + \sqrt{3} \over 4 \sqrt{2}}$$ (8)

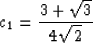$$c_1 = {3 + \sqrt{3} \over 4 \sqrt{2}}$$ (9)

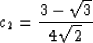$$c_2 = {3 - \sqrt{3} \over 4 \sqrt{2}}$$ (10)

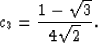$$c_3 = {1 - \sqrt{3} \over 4 \sqrt{2}} .$$ (11)