Further metamorphosis of the elastic wave equation

I believe it is useful to extend the visco-elastic equation in two directions:

• Replace the scalar mass density, 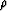$\rho$, with a 3-by-3 matrix representation, R, of a (generally anisotropic) 2nd order inertia tensor.
• Allow frequency-dependence in the elements of the matrix R.

Why do I want to do this? A simple, one-dimensional answer is that velocity and impedance can only be independently controlled by access to both elasticity and density. This is certainly true at the frequency origin, and may also be true just away from the origin.

So, the scalar density in equation (2) is replaced by an inertia matrix, R,

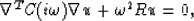$$\nabla ^{T} C(i \omega ) \nabla u + \omega ^{2} R u = 0,$$ (3)

and then this inertia matrix is made frequency dependent:

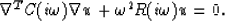$$\nabla ^{T} C(i \omega ) \nabla u + \omega ^{2} R(i \omega ) u = 0.$$ (4)