




Next: Further metamorphosis of the
Up: Muir: Inertia tensor
Previous: Muir: Inertia tensor
This Short Note is part of a continuing effort to extend equivalent medium
theory from the quasi-static and kinematic to the dynamic. In other words
to extend its area of practical application. Backus (1962) taught us how
to add fine-layered isotropic and transverse-isotropic materials, and
Schoenberg & Muir (1989) extended this result to arbitrary anisotropy
and fractures, and introduced a group theory and calculus to systematize
the process. But however useful these results are, they do not speak to the
problem of wavelet broadening, which was addressed so eloquently by
O'Doherty & Anstey (1971).
There is a general understanding by workers in this area that a useful
notion is to model the loss of energy from the coherent field to the
scattered field (which does not place at 0 Hz) by replacing the elastic
wave equation in Helmholtz form,
| 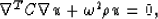 |
(1) |
by a standard form of the visco-elastic equation:
| 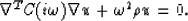 |
(2) |
That is, the elastic matrix (stiffness tensor) C is replaced by a
frequency-dependent form, 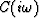 .
.





Next: Further metamorphosis of the
Up: Muir: Inertia tensor
Previous: Muir: Inertia tensor
Stanford Exploration Project
11/17/1997