




Next: Future research
Up: EXAMPLES
Previous: Constant velocity gradient
In this example, I try to break my code on the Marmousi velocity model,
pictured in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The top panel is the true velocity
model, and the lower panel is a 2-D smoothed version (150 m wavelength) I
used for forward modeling traveltimes. Some smoothing is required to
satisfy the ray validity conditions of the eikonal equation
(Cervený et al. (1977)), which most finite difference traveltime algorithms
neglect. Velocity smoothing, ray validity conditions,
and stable numerical evaluation of the eikonal equation as a function of
classes of velocity models, are topics of utmost importance in traveltime
calculation which are not presently well understood.
. The top panel is the true velocity
model, and the lower panel is a 2-D smoothed version (150 m wavelength) I
used for forward modeling traveltimes. Some smoothing is required to
satisfy the ray validity conditions of the eikonal equation
(Cervený et al. (1977)), which most finite difference traveltime algorithms
neglect. Velocity smoothing, ray validity conditions,
and stable numerical evaluation of the eikonal equation as a function of
classes of velocity models, are topics of utmost importance in traveltime
calculation which are not presently well understood.
I used the hybrid finite difference local raytracing algorithm of Zhang (1992)
to forward model traveltimes. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the traveltime field
for a source at
show the traveltime field
for a source at 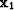 = 4.75 km (upper panel), and a source at
= 4.75 km (upper panel), and a source at 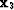 = 5.25 km
(lower panel). The contours show some areas, particularly in the lower panel
near (x,z) = (3.0, 2.2) km, where there are significant traveltime
changes from
= 5.25 km
(lower panel). The contours show some areas, particularly in the lower panel
near (x,z) = (3.0, 2.2) km, where there are significant traveltime
changes from 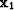 to
to 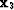 - a shot separation of 500 m. Due to this
large change in traveltime behavior, and the cusp-like nature of the
crossing traveltime branches in the lower panel, we can imagine that these
areas will be difficult to interpolate, and they are. Figure
- a shot separation of 500 m. Due to this
large change in traveltime behavior, and the cusp-like nature of the
crossing traveltime branches in the lower panel, we can imagine that these
areas will be difficult to interpolate, and they are. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the traveltime gradients at source
shows the traveltime gradients at source 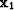 , and Figure
, and Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the traveltime gradients at source
shows the traveltime gradients at source 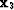 . These
. These 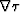 fields
are amazingly discontinuous and predict trouble ahead.
fields
are amazingly discontinuous and predict trouble ahead.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the interpolated traveltime field for a source at
5.0 km. The lower panel shows the relative traveltime error in 5% contour
intervals. The good news is that most of the subsurface region (uncontoured)
has relative traveltime errors of less than 1%, at a fraction of the cost and
disk storage compared to the modeling code.
The bad news is that the corner regions at far offset and
large depths are contaminated with traveltime errors in the range of
5-20%. Figure
shows the interpolated traveltime field for a source at
5.0 km. The lower panel shows the relative traveltime error in 5% contour
intervals. The good news is that most of the subsurface region (uncontoured)
has relative traveltime errors of less than 1%, at a fraction of the cost and
disk storage compared to the modeling code.
The bad news is that the corner regions at far offset and
large depths are contaminated with traveltime errors in the range of
5-20%. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) explains it all. At wide offsets, with sharp
velocity contrasts still remaining in the smoothed Marmousi model, complicated
interactions between head waves and precritical refractions are causing large
traveltime gradient contrasts. In this region, even my enhanced
explains it all. At wide offsets, with sharp
velocity contrasts still remaining in the smoothed Marmousi model, complicated
interactions between head waves and precritical refractions are causing large
traveltime gradient contrasts. In this region, even my enhanced 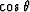 estimate is breaking down, causing the evidenced traveltime instability.
As the traveltimes are spatially integrated through these bad zones, the error
is smeared out to larger depths and offsets.
estimate is breaking down, causing the evidenced traveltime instability.
As the traveltimes are spatially integrated through these bad zones, the error
is smeared out to larger depths and offsets.
However, before I sound the death knell, let's review. The algorithm did
a fine interpolation for a large part of the Marmousi model. The interpolation
was done at a 500 m shot spacing over a very complex velocity structure.
Presently the interpolation code runs at about 4 times the speed of the
traveltime forward modeling code, and I have made zero effort to optimize it.
There is some traveltime gradient interpolation instability in regions of
large and rapid velocity contrast that remain to be understood and overcome.
These instabilities caused relative errors of 5-20% in the worst regions.





Next: Future research
Up: EXAMPLES
Previous: Constant velocity gradient
Stanford Exploration Project
11/17/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The top panel is the true velocity
model, and the lower panel is a 2-D smoothed version (150 m wavelength) I
used for forward modeling traveltimes. Some smoothing is required to
satisfy the ray validity conditions of the eikonal equation
(Cervený et al. (1977)), which most finite difference traveltime algorithms
neglect. Velocity smoothing, ray validity conditions,
and stable numerical evaluation of the eikonal equation as a function of
classes of velocity models, are topics of utmost importance in traveltime
calculation which are not presently well understood.
. The top panel is the true velocity
model, and the lower panel is a 2-D smoothed version (150 m wavelength) I
used for forward modeling traveltimes. Some smoothing is required to
satisfy the ray validity conditions of the eikonal equation
(Cervený et al. (1977)), which most finite difference traveltime algorithms
neglect. Velocity smoothing, ray validity conditions,
and stable numerical evaluation of the eikonal equation as a function of
classes of velocity models, are topics of utmost importance in traveltime
calculation which are not presently well understood.