Next: Constant velocity gradient
Up: EXAMPLES
Previous: EXAMPLES
The first example is a constant velocity model of 2.0 km/s and dimensions
of 6 km on a side. The first known source position is at 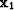 = 0.0 km, and
the second known source position is at
= 0.0 km, and
the second known source position is at 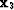 = 6.0 km, which represents
a very sparse traveltime table spatial separation of 6 km. (Of course, for
constant velocity and v(z) models, the traveltimes depend only on offset
and depth, and are independent of lateral source position. In this regard,
the comment on sparse sampling is relevant only in terms of interpolation,
and is not relevant to what I would actually do in practice!)
Their respective
traveltime fields
= 6.0 km, which represents
a very sparse traveltime table spatial separation of 6 km. (Of course, for
constant velocity and v(z) models, the traveltimes depend only on offset
and depth, and are independent of lateral source position. In this regard,
the comment on sparse sampling is relevant only in terms of interpolation,
and is not relevant to what I would actually do in practice!)
Their respective
traveltime fields 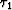 and
and 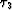 are plotted in Figure
are plotted in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The horizontal and vertical traveltime gradient fields at
.
The horizontal and vertical traveltime gradient fields at 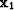 are denoted as
are denoted as
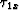 and
and 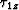 respectively, and are plotted in Figure
respectively, and are plotted in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The horizontal and vertical traveltime gradient fields at
.
The horizontal and vertical traveltime gradient fields at 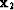 are denoted as
are denoted as
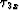 and
and 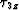 respectively, and are plotted in Figure
respectively, and are plotted in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
The interpolated traveltime field 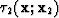 at
at 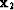 = 3.0 km is plotted in the top panel of Figure
= 3.0 km is plotted in the top panel of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , and
the traveltime gradients
, and
the traveltime gradients 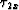 and
and 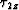 are plotted in Figure
are plotted in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The relative interpolation traveltime error is
contoured in the lower panel of Figure
. The relative interpolation traveltime error is
contoured in the lower panel of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The contour farthest
from the desired source position at 3.0 km has a value of 1%, and increases
to 10% relative error as you move in toward the source position, in
1% contour value increments.
In theory, this example should be error-free since the
. The contour farthest
from the desired source position at 3.0 km has a value of 1%, and increases
to 10% relative error as you move in toward the source position, in
1% contour value increments.
In theory, this example should be error-free since the 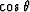 terms
are given exactly by (8) in a constant velocity medium.
For this example, the interpolated traveltimes are
accurate to within 1% relative error, my rule of thumb requirement, over
most of the subsurface space, using a sparse shot interval of 6 km.
However, there is evidence of some small numerical inaccuracy and a
resulting tendency of singularity right at the source position, where
the
terms
are given exactly by (8) in a constant velocity medium.
For this example, the interpolated traveltimes are
accurate to within 1% relative error, my rule of thumb requirement, over
most of the subsurface space, using a sparse shot interval of 6 km.
However, there is evidence of some small numerical inaccuracy and a
resulting tendency of singularity right at the source position, where
the 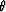 values change rapidly and are therefore most sensitive to error.
Hence, in more general velocity models, we should expect instability near the
source region.
values change rapidly and are therefore most sensitive to error.
Hence, in more general velocity models, we should expect instability near the
source region.
c13t
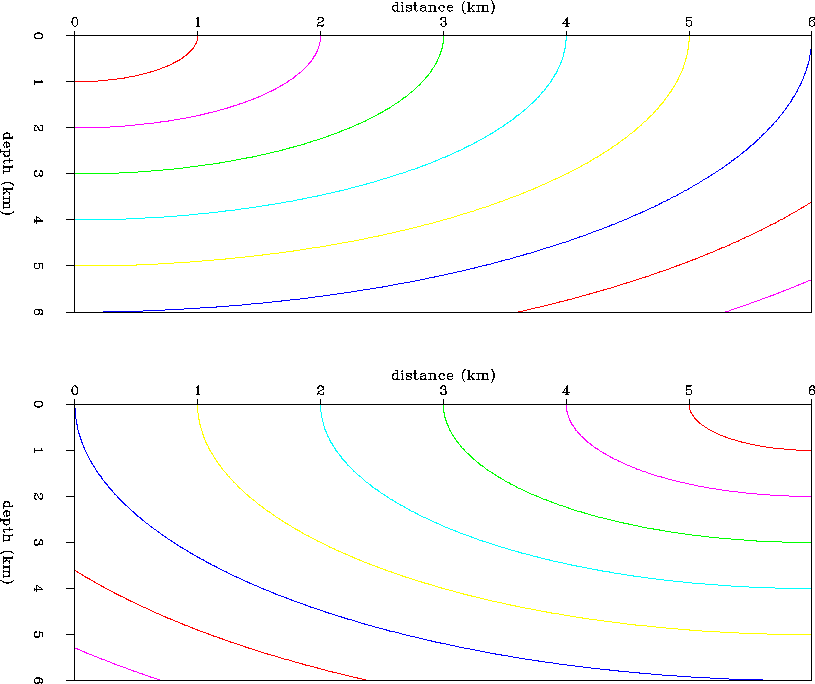
Figure 2 Constant velocity model.
Contours of traveltime field for
the two given surface source positions at 0.0 km (top) and 6.0 km
(bottom).




 c1xz
c1xz
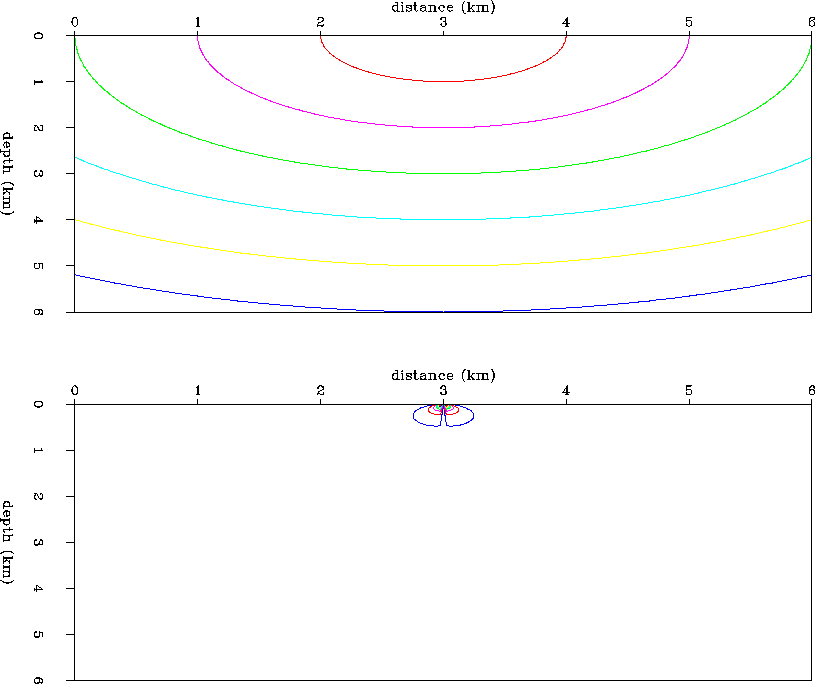
Figure 3 Constant velocity model.
Horizontal (top) and vertical
(bottom) traveltime gradient fields for
the surface source positioned at 0.0 km.




 c3xz
c3xz
Figure 4 Constant velocity model.
Horizontal (top) and vertical
(bottom) traveltime gradient fields for
the surface source positioned at 6.0 km.




 cite
cite
Figure 5 Constant velocity model.
Interpolated traveltime field.
The top panel is the interpolated traveltime field for a surface
source positioned at 3.0 km. The lower panel is the relative
error between the interpolated traveltime field, and the correct
traveltimes modeled by an analytical solution to the eikonal. The
contour farthest from the source region is at 1% relative error,
and the contour values increase to 10% error right at the source
location, in 1% contour increments.




 cixz
cixz
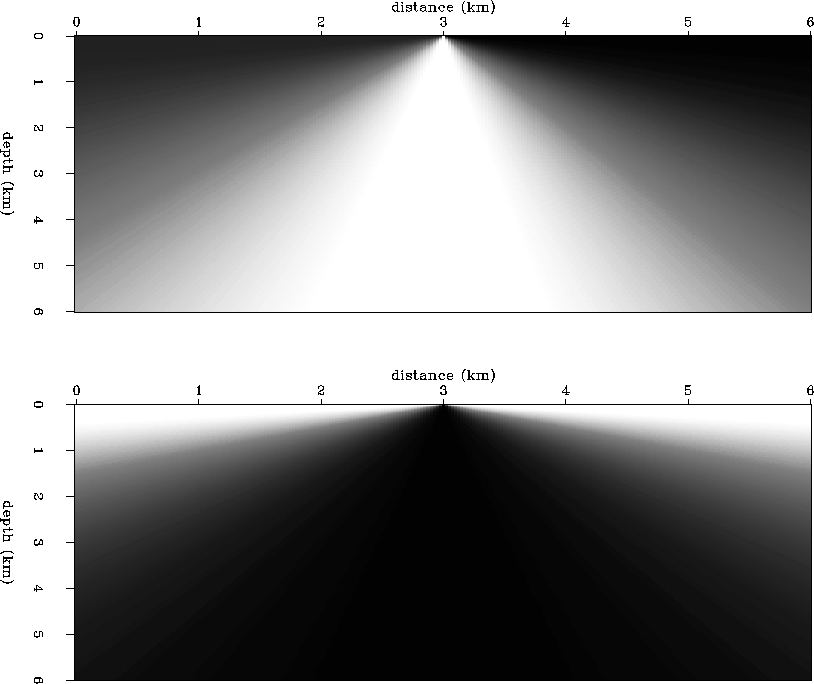
Figure 6 Constant velocity model.
Horizontal (top) and vertical
(bottom) traveltime gradient fields for
the interpolated surface source positioned at 3.00 km.










Next: Constant velocity gradient
Up: EXAMPLES
Previous: EXAMPLES
Stanford Exploration Project
11/17/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The horizontal and vertical traveltime gradient fields at
.
The horizontal and vertical traveltime gradient fields at ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The horizontal and vertical traveltime gradient fields at
.
The horizontal and vertical traveltime gradient fields at ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![]() = 0.0 km, and
the second known source position is at
= 0.0 km, and
the second known source position is at ![]() = 6.0 km, which represents
a very sparse traveltime table spatial separation of 6 km. (Of course, for
constant velocity and v(z) models, the traveltimes depend only on offset
and depth, and are independent of lateral source position. In this regard,
the comment on sparse sampling is relevant only in terms of interpolation,
and is not relevant to what I would actually do in practice!)
Their respective
traveltime fields
= 6.0 km, which represents
a very sparse traveltime table spatial separation of 6 km. (Of course, for
constant velocity and v(z) models, the traveltimes depend only on offset
and depth, and are independent of lateral source position. In this regard,
the comment on sparse sampling is relevant only in terms of interpolation,
and is not relevant to what I would actually do in practice!)
Their respective
traveltime fields ![]() and
and ![]() are plotted in Figure
are plotted in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The horizontal and vertical traveltime gradient fields at
.
The horizontal and vertical traveltime gradient fields at ![]() are denoted as
are denoted as
![]() and
and ![]() respectively, and are plotted in Figure
respectively, and are plotted in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The horizontal and vertical traveltime gradient fields at
.
The horizontal and vertical traveltime gradient fields at ![]() are denoted as
are denoted as
![]() and
and ![]() respectively, and are plotted in Figure
respectively, and are plotted in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![]() at
at ![]() = 3.0 km is plotted in the top panel of Figure
= 3.0 km is plotted in the top panel of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , and
the traveltime gradients
, and
the traveltime gradients ![]() and
and ![]() are plotted in Figure
are plotted in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The relative interpolation traveltime error is
contoured in the lower panel of Figure
. The relative interpolation traveltime error is
contoured in the lower panel of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The contour farthest
from the desired source position at 3.0 km has a value of 1%, and increases
to 10% relative error as you move in toward the source position, in
1% contour value increments.
In theory, this example should be error-free since the
. The contour farthest
from the desired source position at 3.0 km has a value of 1%, and increases
to 10% relative error as you move in toward the source position, in
1% contour value increments.
In theory, this example should be error-free since the ![]() terms
are given exactly by (8) in a constant velocity medium.
For this example, the interpolated traveltimes are
accurate to within 1% relative error, my rule of thumb requirement, over
most of the subsurface space, using a sparse shot interval of 6 km.
However, there is evidence of some small numerical inaccuracy and a
resulting tendency of singularity right at the source position, where
the
terms
are given exactly by (8) in a constant velocity medium.
For this example, the interpolated traveltimes are
accurate to within 1% relative error, my rule of thumb requirement, over
most of the subsurface space, using a sparse shot interval of 6 km.
However, there is evidence of some small numerical inaccuracy and a
resulting tendency of singularity right at the source position, where
the ![]() values change rapidly and are therefore most sensitive to error.
Hence, in more general velocity models, we should expect instability near the
source region.
values change rapidly and are therefore most sensitive to error.
Hence, in more general velocity models, we should expect instability near the
source region.