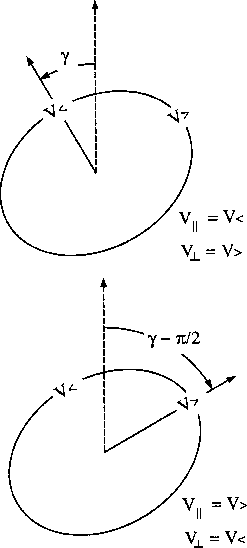
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows how
a given ellipse can be described with two different sets
of parameters.
shows how
a given ellipse can be described with two different sets
of parameters.
Every ellipse has two axes of symmetry. The inversion proposed in this paper can estimate the inclination with respect to the vertical of either one of them depending on which axis is closer to the initial model. In either case, the estimated parameters will always describe the same elliptical velocity function.
Another way to understand why
the inversion can estimate the inclination of either axis of symmetry
is by examining the traveltime equation (1).
An identical equation
can be obtained
if we switch in (1) ![]() and
and ![]() changing
at the same time
changing
at the same time ![]() by
by ![]() . This means
that the traveltimes are affected only
by
the elliptical function
of velocities regardless of how such a function is described.
Figure
. This means
that the traveltimes are affected only
by
the elliptical function
of velocities regardless of how such a function is described.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows how
a given ellipse can be described with two different sets
of parameters.
shows how
a given ellipse can be described with two different sets
of parameters.
If the inversion procedure is forced to estimate the same axis of the ellipse (either the major or the minor) for every layer, it can be more difficult (or impossible) to get a reliable estimate of the real elliptical velocity function of the medium, especially in cases when the axis of symmetry in the initial model is far from the true answer.
 |