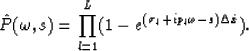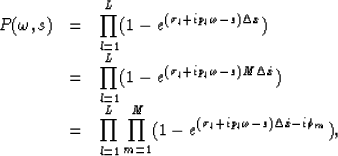Next: Dealiasing prediction filters with
Up: DEALIASING THE PREDICTION FILTERS
Previous: DEALIASING THE PREDICTION FILTERS
Because prediction filters are finite-impulse-response filters, they
can be characterized by the zeros of their z-transform.
From equation (2), we know
that the zeros of the prediction filter
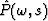 are
are 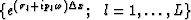 .Therefore, we can express this filter as follows:
.Therefore, we can express this filter as follows:
| 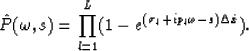 |
(10) |
If we scan the amplitude spectrum of this filter over the s plane,
we can find L notches at
|  |
(11) |
that locate all the zeros of the z-transform of this filter.
Similarly, we can express the prediction filter 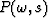 as follows:
as follows:
| 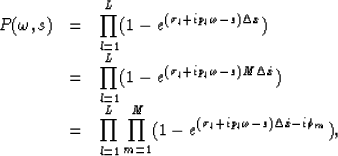 |
(12) |
where 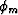 denotes the phases of the Mth order complex roots of
the unity. Now, if we scan the amplitude spectrum of
denotes the phases of the Mth order complex roots of
the unity. Now, if we scan the amplitude spectrum of 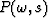 over
the s plane, we can
find
over
the s plane, we can
find 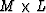 notches at
notches at
| 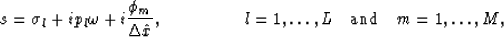 |
(13) |
M times as many notches as that of 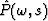 .Comparing equation (13) with equation (11),
it is apparent that these two equations become identical
when
.Comparing equation (13) with equation (11),
it is apparent that these two equations become identical
when 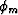 is equal to zero. Thus, L out of
is equal to zero. Thus, L out of 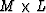 zeros
of
zeros
of 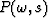 are the zeros of
are the zeros of 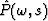 .Our goal is to identify these L zeros when
.Our goal is to identify these L zeros when 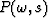 is known.
If the component of data at frequency
is known.
If the component of data at frequency 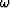 is not spatially aliased, then
is not spatially aliased, then
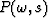 has L zeros between two vertical lines
has L zeros between two vertical lines 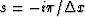 and
and 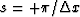 , which are L zeros of
, which are L zeros of 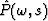 . However,
if the component of data at frequency
. However,
if the component of data at frequency 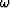 is spatially aliased,
the task of identifying the zeros becomes complicated and requires
sophisticated algorithms.
is spatially aliased,
the task of identifying the zeros becomes complicated and requires
sophisticated algorithms.





Next: Dealiasing prediction filters with
Up: DEALIASING THE PREDICTION FILTERS
Previous: DEALIASING THE PREDICTION FILTERS
Stanford Exploration Project
11/18/1997
![]() are
are ![]() .Therefore, we can express this filter as follows:
.Therefore, we can express this filter as follows: