Next: CONCLUSIONS
Up: REGRIDDING IRREGULARLY SAMPLED TRACES
Previous: REGRIDDING IRREGULARLY SAMPLED TRACES
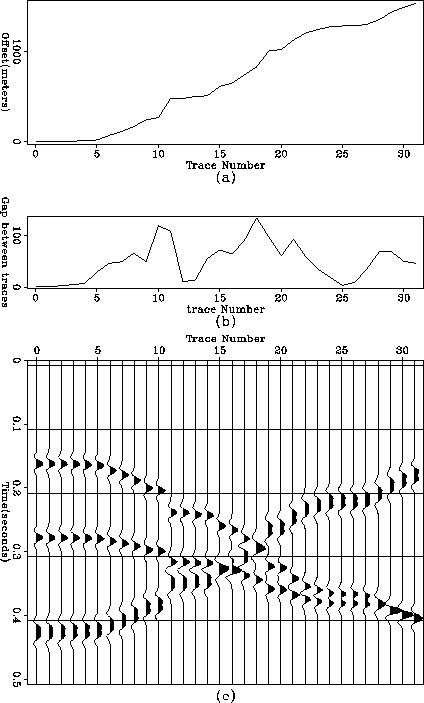
For testing of this algorithm, a synthetic data set containing four
linear events without noises, shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c, is prepared.
This synthetic data set is irregularly sampled along the offset axis,
while the offsets, shown in Figure
c, is prepared.
This synthetic data set is irregularly sampled along the offset axis,
while the offsets, shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a, do not increase linearly with
respect to the trace number.
For a clearer understanding of the geometry of Figure
a, do not increase linearly with
respect to the trace number.
For a clearer understanding of the geometry of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c,
I include Figure
c,
I include Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b, which is the gap between traces and it shows
a random characteristic of the trace offsets.
Figure
b, which is the gap between traces and it shows
a random characteristic of the trace offsets.
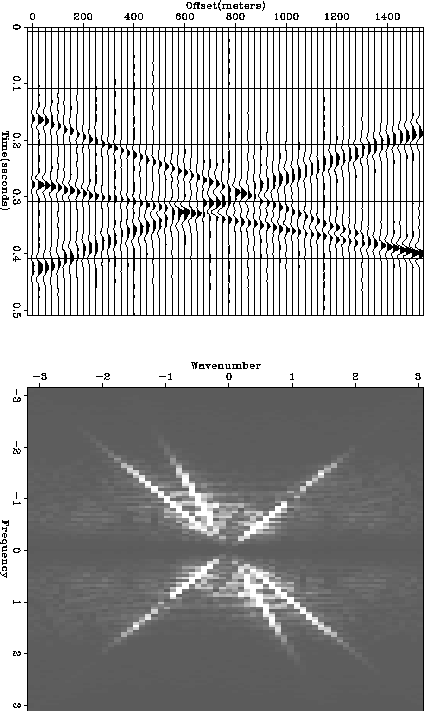
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the result of regridding with uniform sampling interval
of the data shown in Figure
shows the result of regridding with uniform sampling interval
of the data shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c.
Even though the result produced some noises which did not exist in the
original data set, all linear events show good line up with dips picked,
and the spectrum in Figure
c.
Even though the result produced some noises which did not exist in the
original data set, all linear events show good line up with dips picked,
and the spectrum in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) confirms a reasonable interpolation.
confirms a reasonable interpolation.
For a more realistic example, noises have been added to the data set,
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c, and it is shown in Figure
c, and it is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c.
The offsets of traces in this data set are the same as the data set
without noise.
Figure
c.
The offsets of traces in this data set are the same as the data set
without noise.
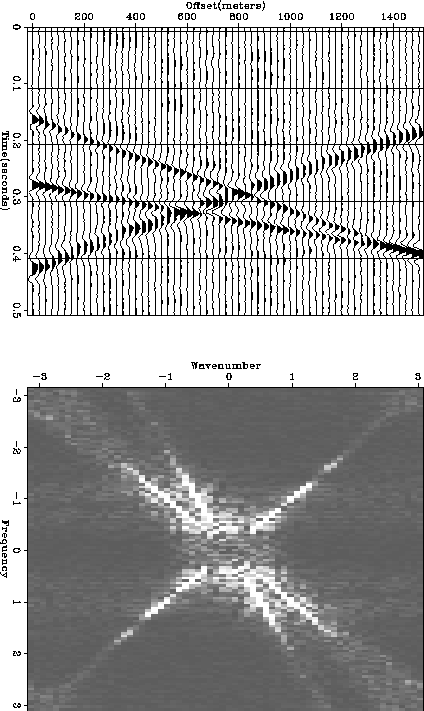
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the result after regridding from Figure
shows the result after regridding from Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c,
and also good line up along dips picked.
c,
and also good line up along dips picked.
irrdat
Figure 8 (a) Offset with respect to the trace number.
(b) Offset difference between the nearest traces.
(c) Synthetic plane waves with irregularly sampled traces and the
zero traces are regularly sampled trace which is to interpolated.




 irrint
irrint
Figure 9 (a) The result of interpolation onto a uniformly sampled grid(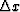 = 25 meters).
(b) the spectrum of (a)
= 25 meters).
(b) the spectrum of (a)
 irrdatwn
irrdatwn
Figure 10 (a) Offset with respect to the trace number.
(b) Offset difference between the nearest traces.
(c) Synthetic plane waves with irregularly sampled traces and the
zero traces are regularly sampled trace which is to interpolated.




 irrwnint
irrwnint
Figure 11 (a) The result of interpolation onto a uniformly sampled grid(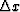 = 25 meters).
(b) the spectrum of (a)
= 25 meters).
(b) the spectrum of (a)






Next: CONCLUSIONS
Up: REGRIDDING IRREGULARLY SAMPLED TRACES
Previous: REGRIDDING IRREGULARLY SAMPLED TRACES
Stanford Exploration Project
11/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c, and it is shown in Figure
c, and it is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c.
The offsets of traces in this data set are the same as the data set
without noise.
Figure
c.
The offsets of traces in this data set are the same as the data set
without noise.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the result after regridding from Figure
shows the result after regridding from Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c,
and also good line up along dips picked.
c,
and also good line up along dips picked.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c, is prepared.
This synthetic data set is irregularly sampled along the offset axis,
while the offsets, shown in Figure
c, is prepared.
This synthetic data set is irregularly sampled along the offset axis,
while the offsets, shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a, do not increase linearly with
respect to the trace number.
For a clearer understanding of the geometry of Figure
a, do not increase linearly with
respect to the trace number.
For a clearer understanding of the geometry of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c,
I include Figure
c,
I include Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b, which is the gap between traces and it shows
a random characteristic of the trace offsets.
Figure
b, which is the gap between traces and it shows
a random characteristic of the trace offsets.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the result of regridding with uniform sampling interval
of the data shown in Figure
shows the result of regridding with uniform sampling interval
of the data shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c.
Even though the result produced some noises which did not exist in the
original data set, all linear events show good line up with dips picked,
and the spectrum in Figure
c.
Even though the result produced some noises which did not exist in the
original data set, all linear events show good line up with dips picked,
and the spectrum in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) confirms a reasonable interpolation.
confirms a reasonable interpolation.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c, and it is shown in Figure
c, and it is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c.
The offsets of traces in this data set are the same as the data set
without noise.
Figure
c.
The offsets of traces in this data set are the same as the data set
without noise.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the result after regridding from Figure
shows the result after regridding from Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c,
and also good line up along dips picked.
c,
and also good line up along dips picked.