![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) I use lomoplan()
I use lomoplan() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) to solve for the array
of prediction-error filters A in
to solve for the array
of prediction-error filters A in
Given some initial data d0 with missing traces
filled by gapfill() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) I use lomoplan()
I use lomoplan() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) to solve for the array
of prediction-error filters A in
to solve for the array
of prediction-error filters A in
| (3) | ||
| (4) |
I will not have courage to begin the iterative migrations
until I am able to define everything
so that the ![]() -planes seem to have the general
character of the removed data.
A problem above is that
-planes seem to have the general
character of the removed data.
A problem above is that ![]() beats down all
the coefficients in the model A, and I wish it was
more selective.
Below is the filter I began with.
beats down all
the coefficients in the model A, and I wish it was
more selective.
Below is the filter I began with.
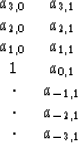 |
(5) |
There was much too much high frequency in ![]() ,because, as you see, the inverse covariance matrix appears twice
in
,because, as you see, the inverse covariance matrix appears twice
in ![]() .In ordinary deconvolution, we may gap the filter to avoid
an output dominated by near Nyquist frequencies.
Thus I experimented with gapping this filter,
and I decided to work with
.In ordinary deconvolution, we may gap the filter to avoid
an output dominated by near Nyquist frequencies.
Thus I experimented with gapping this filter,
and I decided to work with
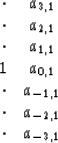 |
(6) |
Inspecting the ![]() -plane I saw too much unrealistically steep dip.
First I thought, maybe the semicircular smiles need it.
Then I realized, our concern is defects in the data plane,
not the model plane.
So I decided to cut back on the number of filter coefficients
to match that in Claerbout Claerbout (1992c).
Thus, finally, I am working with the filter
-plane I saw too much unrealistically steep dip.
First I thought, maybe the semicircular smiles need it.
Then I realized, our concern is defects in the data plane,
not the model plane.
So I decided to cut back on the number of filter coefficients
to match that in Claerbout Claerbout (1992c).
Thus, finally, I am working with the filter
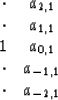 |
(7) |
Figures 1 and 2 show the ingredients
of ![]() .Since figure captions do not seem tolerant of mathematics
these days I will explain here that the left column
is without missing data.
The 6 panels, in vertical order, are
Md,
d+g (g is unknown data estimated by the gapfill program),
K(d+g),
AK(d+g),
A'AK(d+g) and
.Since figure captions do not seem tolerant of mathematics
these days I will explain here that the left column
is without missing data.
The 6 panels, in vertical order, are
Md,
d+g (g is unknown data estimated by the gapfill program),
K(d+g),
AK(d+g),
A'AK(d+g) and
![]() .
.
 |