PROCESSING AS CONJUGATE TO FIELD OPERATION

Knowing how data is recorded, or how we would like it to be recorded, suggests various possibilities for data processing. Should we ignore the little rectangle functions, or should we include them in the data processing? Figure 2 shows a simple model and its implied data, along with migrations, with and without attention to aliasing the horizontal space axis. The figure shows that migration without attention to aliasing leads to systematic noise and (apparently) random noise.

 

migalias
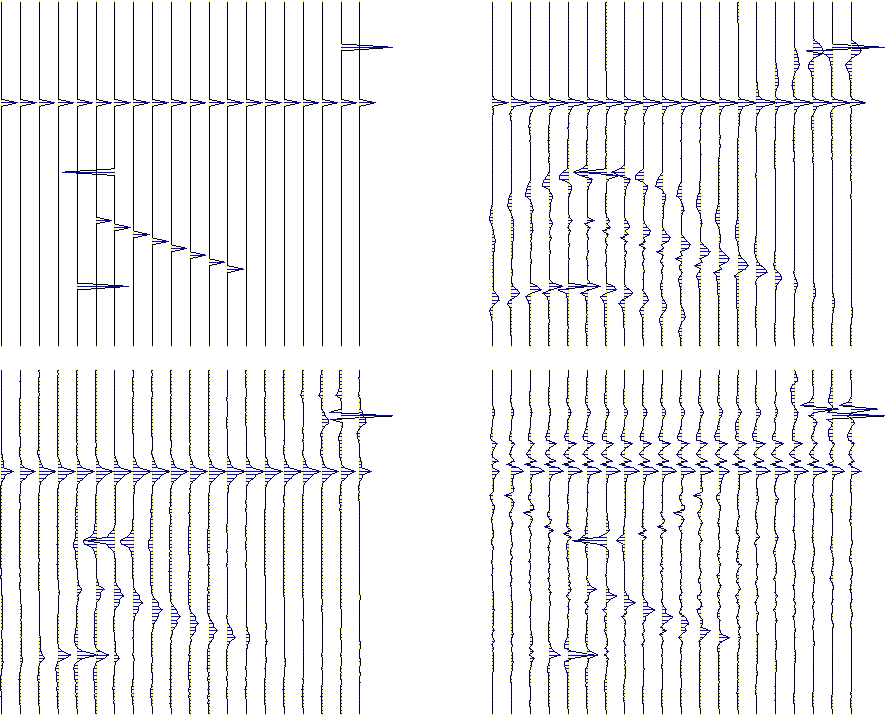
Figure 2 Top left is a synthetic image. Top right is synthetic data from the synthetic image. Bottom are migrations of the data with and without antialiasing.

This figure is based on realistic parameters except that I compute and display the results on a very coarse mesh ($20\times 100$)to enable you to see clearly the phenomena of numerical analysis. No additional values were used between mesh points or off the edges of what is shown.

Fourier and finite-difference methods of migration seem to be immune to an aliasing malady suffered by hyperbola summation (Kirchhoff) migration. Here we limit our studies to Kirchhoff-type migrations. We will see a simple method to overcome this ``operator-aliasing'' malady. Operator aliasing should not be confused with data aliasing which is a deeper malady for which there is no direct cure.

The practical need to limit operator aliasing is often reduced by three indirect measures. First is temporal low pass filtering which has the unfortunate side effect of reducing the temporal bandwidth. Second is dip limiting (limiting the aperture of the hyperbola) which has the unfortunate side effect of limiting the dip bandwidth. Third is interlacing the data traces. Interpolating the data also interpolates the operator so if enough trace interpolation is done, the operator is no longer subsampled. A disadvantage of data interpolation is that the data becomes more bulky. Here we attack the operator aliasing problem directly.

Look at Figure 3. Note that in some places each value of x corresponds to several values of t, and other places it is the opposite where one value of t corresponds to several values of x. An aliasing problem arises when we approximate a line integral by a simple sum of points, one for each value on the x-axis instead of using the more complicated trajectory that you see in Figure 3.

 

nmotraj Figure 3 To integrate along hyperbolas without aliasing, you should include (at least) the points shown.

A simple program designed for antialiasing gave the result in Figure 4. A zero-offset signal is input to conjugate NMO to make synthetic data which is then NMO'ed and stacked. Notice that the end of each rectangle is the beginning of the rectangle at the next offset.

 

boxmo1 Figure 4 Rectangle smoothing during NMO and stacking. Notice that the end of one rectangle exactly coincides with the beginning of the rectangle at next larger offset. Thus, rectangle width increases with offset and decreases with time. (antialias=1.)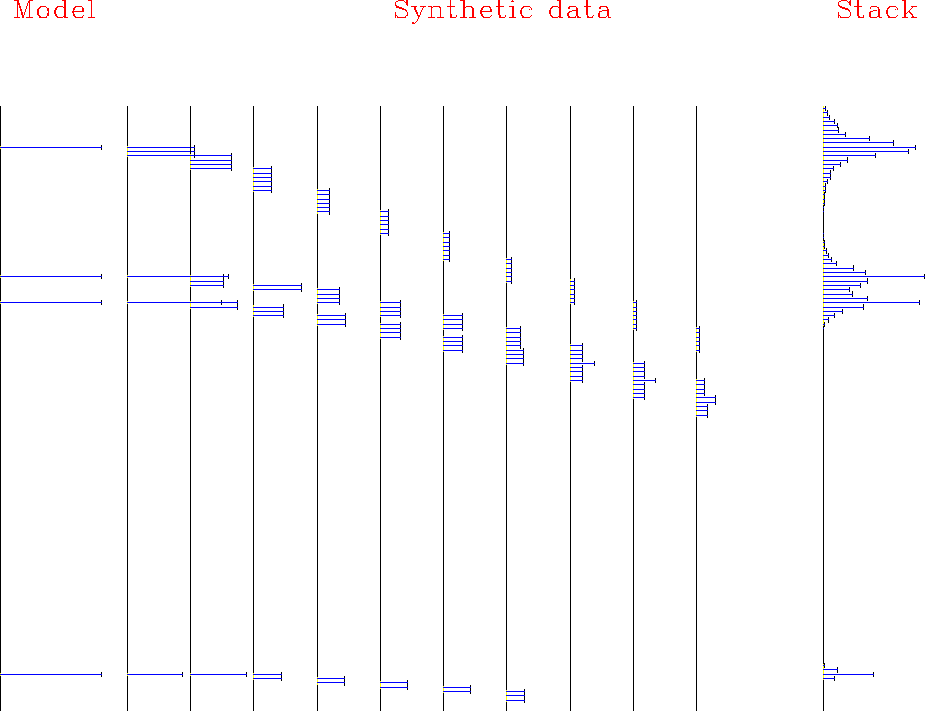

You might fear the coding that led up to Figure 4 is a fussy and inefficient business because of all the short little summation loops. Luckily, there is a marvelous little formula that allows us to express the integral under any of the little rectangles, no matter how many points it contains, by a single subtraction. Integration is the key. It is only necessary to realize that the sums are, like a definite integral, representable by the difference of the indefinite integral at each end. In other words, to find the sum of all the values between it and it+n we begin with a recursive summation such as qq(it)=qq(it-1)+pp(it). Then, any sum of values like pp(it)++p(it+n) is simply qq(it)-qq(it+n+1).

Figure 4 is not fully consistent with Figure 3. In Figure 4 notice that the last point in each rectangular area overlaps the next rectangular area by one point. Overlap could be avoided by shortening each rectangle by one point, but then rectangles near the apex of the hyperbola would have zero length which is wholly unacceptable. Should we write a code to match Figure 3? This would be better, but far from perfect. Notice in Figure 3 that a horizontal sum of the number of boxes is not a smooth function of time. To achieve more smoothness, we later turn to triangles, but first we look at some implementation details for rectangles.