ARTIFACTS

Reconstructing the earth model with the conjugate option in kirchfast() yields the result in Figure 2.

 

skmig
Figure 2 Left is the original model Right is the reconstruction.

The reconstruction generally succeeds but is imperfect in a number of interesting ways. Near the bottom and right side, the reconstruction fades away especially where the dips are steeper. Bottom fading results because in modeling the data we abandoned arrivals after a certain maximum time. Thus energy needed to reconstruct dipping beds near the bottom was abandoned. Likewise along the side we abandoned rays shooting off the frame.

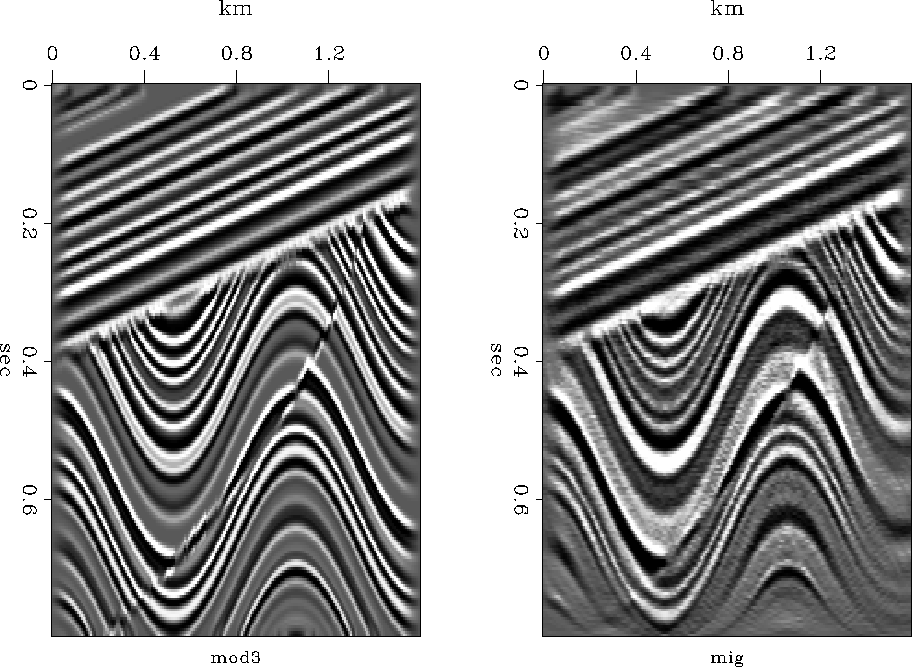Difficult migrations are well known for producing semicircular reflectors. Here we have controlled everything fairly well so none are obvious, but on a video screen I see some semicircles.

Next is the problem of the spectrum. Notice in Figure 2 that the reconstruction lacks the sharp crispness of the original. It can be shown mathematically that the spectrum of our reconstruction loses high frequencies by a scale of about $1/ \vert \omega \vert$.Philosophically, we can think of the integration as boosting low frequencies. Figure 3 shows the average over x of the relevant spectra.

 

kirspec Figure 3 Top is the spectrum of the left side of Figure 2. Bottom is the spectrum of the right side of Figure 2. Middle is bottom times frequency.

First, notice the high frequencies are weak because there is little high frequency energy in the original model. Then notice that our cavalier approach to interpolation created more high frequency energy. Finally, notice that multiplying the spectrum of our migrated model by frequency, f, brought the important part of the spectral bands into agreement. This suggest applying an $\vert\omega \vert$ filter to our reconstruction, or $\sqrt{-i\omega}$ operator to both the modeling and the reconstruction. We will take that up somewhere else.

Neither of these Kirchhoff codes addresses the issue of spatial aliasing. Spatial aliasing is a vexing issue of numerical analysis. The Kirchhoff codes shown here do not work as expected unless the space mesh size is suitably more refined than the time mesh. Figure 4 shows an example of forward modeling with a spatial mesh of 50 and 100 points.

 

skmod
Figure 4 Left is model. Right is synthetic data from the model. Top has 50 points on the x-axis, bottom has 100.

(Previous figures used 200 points on space. All use 200 mesh points on the time.) Subroutine kirchfast() does interpolation by moving values to the nearest neighbor of the theoretical location. Had we taken the trouble to interpolate the two nearest points, our results would have been a little better, but the basic problem (resolved in jon/res/trimo) would remain.