Cross-well data

The cross-well data donated by the Stanford Tomography Project (STP) is used to test the algorithm. The shot gather (Figure ) consists of 316 traces, each containing 512 time samples. The traces are 1 foot apart and are sampled at 0.2 ms. The shot was at 540 foot depth. In order to test the interpolation algorithm, the data set was decimated by removing every other trace (Figure ). This spatially aliases the data and gives it a rougher checkerboard appearance. A plot of the spectrum (Figure ) clearly shows the aliased energy.

 

cwldat
Figure 5 Cross-well data set before decimation. The trace separation is 1 foot.

 

cwldec
Figure 6 Decimated cross-well data set. Every other trace has been removed from the original data set so that the trace separation is 2 feet.

 

cwlalias
Figure 7 Decimated cross-well data set spectrum. The spectrum is tilled between plus and minus twice Nyquist along the wavenumber axis to emphasize the aliased energy.

This data set is nonstationary. In order to perform the interpolation I must apply the algorithm to small windows of data and then piece these back together. This is done by the program Pstri() (Appendix). The data set is split up into 2048 overlapping windows. The shaping filter is calculated and applied in each window. The interpolated windows are then patched back together with triangular weights on each window.

The result of the interpolation is presented in Figure . This compares quite well to Figure . The events are now much smoother and more continuos than in Figure . The higher amplitude events are reconstructed better than the weaker events.

There are artifacts in the interpolation that I have not been able to removing yet. The most distracting artifacts are the oscillations at various points in the interpolated data (such as at depth=740', t=0.11s). These are due to the aliasing of the shaping filter. Median filtering the shaping filter is unsuccessful in removing these artifacts because the shaping filter varies too much in each window. Increasing the number of windows does reduce these artifacts. Some of the fainter steeply dipping tube wave arrivals visible late in the section at depth=700' to depth=800' in Figure  have been removed by the interpolation (Figure ). The tube waves arriving at earlier times have also been attenuated. The algorithm has difficulty reconstructing these arrivals because they are high frequency and relatively low amplitude. Although it is often desirable to remove tube waves from cross-well data, that is not the goal of interpolation.

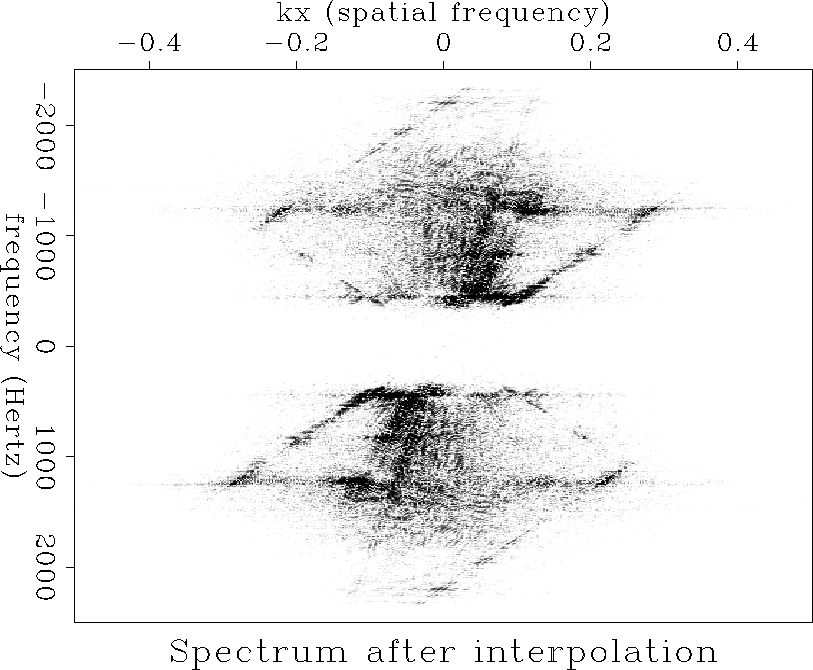
The spectrum of the interpolated cross-well data (Figure ) shows that most of the aliased energy has been removed.

Windowing the data gives rise to a whole set of parameter choices which effect the final quality of the interpolation. In general, increasing the number of windows in which the interpolation is done increases the quality of the interpolation.

I plan to experiment with the shaping filter design in order to eliminate the artifacts due to filter aliasing. Since the effect of the filter aliasing is distinctive, it seems likely that it could be eliminated.

 

intcwl
Figure 8 Interpolated cross-well data. Every other trace has been interpolated so that the trace separation is 1 foot.

 

intcwlfft
Figure 9 Spectrum of the interpolated cross-well data.