




Next: APPLICATION OF THE METHOD
Up: THEORETICAL BACKGROUND
Previous: Calculating the pressure gradient
Using the partial derivatives defined by
equations (15), (17), and (13), we
can express equation (4) as a simple linear operation
in the 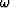 -
-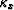 domain:
domain:
| 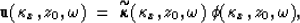 |
(18) |
where 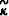 is the vectorizer operator,
whose components are
is the vectorizer operator,
whose components are
| 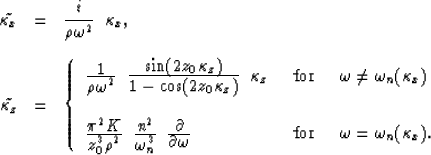 |
(19) |
| (20) |
| (21) |
The horizontal and vertical components of the operator represented
in equations (19) and (21), are
illustrated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) in both the frequency-wavenumber
and the space-time domains. It is important to realize that while Figures
in both the frequency-wavenumber
and the space-time domains. It is important to realize that while Figures
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -a and
-a and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -c multiply the Fourier-transformed
pressure field,
-c multiply the Fourier-transformed
pressure field, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -e multiplies the frequency-derivative
of the same transformed field. Therefore, while
-e multiplies the frequency-derivative
of the same transformed field. Therefore, while ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -b and
-b and
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -d should be convolved with the pressure field,
-d should be convolved with the pressure field,
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -f should be convolved with the time-scaled pressure field
(which is, in practice, equivalent to convolving it with the wavefield
corrected for 2-D divergence). Only the non-zero parts of the operator
are represented in the figure, that is, the imaginary parts in
-f should be convolved with the time-scaled pressure field
(which is, in practice, equivalent to convolving it with the wavefield
corrected for 2-D divergence). Only the non-zero parts of the operator
are represented in the figure, that is, the imaginary parts in
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -a and
-a and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -f and the real parts in the other four
images.
-f and the real parts in the other four
images.
operator
Figure 1 Wavefield vectorizer operator. (a)  in
in  -
- domain. (b)
domain. (b) 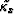 in x-t domain. (c)
in x-t domain. (c) 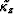 in
in 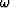 -
-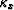 domain (for
domain (for 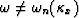 ). (d)
). (d)
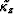 in x-t domain (for
in x-t domain (for 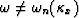 ).
(e)
).
(e) 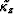 in
in 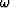 -
-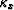 domain (for
domain (for 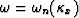 ). (f)
). (f) 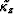 in x-t domain (for
in x-t domain (for 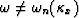 ).
).

It is interesting to observe that the impulse response of 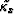 in the space-time domain clearly resembles a second derivative in time
and a first derivative in space. Inverse theory tells us that the first
approximation to the inverse is the conjugate operator, and in this
case we find that the double time integration coming from the
in the space-time domain clearly resembles a second derivative in time
and a first derivative in space. Inverse theory tells us that the first
approximation to the inverse is the conjugate operator, and in this
case we find that the double time integration coming from the 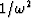 term resembles a second time derivative in the time domain.
term resembles a second time derivative in the time domain.





Next: APPLICATION OF THE METHOD
Up: THEORETICAL BACKGROUND
Previous: Calculating the pressure gradient
Stanford Exploration Project
11/18/1997
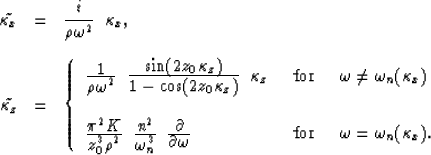
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) in both the frequency-wavenumber
and the space-time domains. It is important to realize that while Figures
in both the frequency-wavenumber
and the space-time domains. It is important to realize that while Figures
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -a and
-a and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -c multiply the Fourier-transformed
pressure field,
-c multiply the Fourier-transformed
pressure field, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -e multiplies the frequency-derivative
of the same transformed field. Therefore, while
-e multiplies the frequency-derivative
of the same transformed field. Therefore, while ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -b and
-b and
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -d should be convolved with the pressure field,
-d should be convolved with the pressure field,
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -f should be convolved with the time-scaled pressure field
(which is, in practice, equivalent to convolving it with the wavefield
corrected for 2-D divergence). Only the non-zero parts of the operator
are represented in the figure, that is, the imaginary parts in
-f should be convolved with the time-scaled pressure field
(which is, in practice, equivalent to convolving it with the wavefield
corrected for 2-D divergence). Only the non-zero parts of the operator
are represented in the figure, that is, the imaginary parts in
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -a and
-a and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -f and the real parts in the other four
images.
-f and the real parts in the other four
images.

![]() in the space-time domain clearly resembles a second derivative in time
and a first derivative in space. Inverse theory tells us that the first
approximation to the inverse is the conjugate operator, and in this
case we find that the double time integration coming from the
in the space-time domain clearly resembles a second derivative in time
and a first derivative in space. Inverse theory tells us that the first
approximation to the inverse is the conjugate operator, and in this
case we find that the double time integration coming from the ![]() term resembles a second time derivative in the time domain.
term resembles a second time derivative in the time domain.