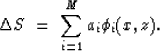Next: SINGULAR VALUE DECOMPOSITION: APPLICATION
Up: Michelena: SVD
Previous: SINGULAR VALUE DECOMPOSITION: SHORT
Regardless of how the model is described, the problem of ray theoretic
traveltime tomography always reduces to the solution of a system of
equations of the form:
| 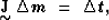 |
(2) |
where 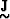 is a matrix whose nature depends on how the
model is described,
is a matrix whose nature depends on how the
model is described, 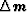 is a vector that
contains the variations in model parameters with
respect to a reference model, and
is a vector that
contains the variations in model parameters with
respect to a reference model, and
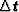 is the misfit between real and calculated
traveltimes.
is the misfit between real and calculated
traveltimes.
The model can be described in many different ways. However, in
this paper I will only focus on three of them .
The first one will be the conventional
discretization of the medium in cells of constant slowness Sj (McMechan,
1983):
| 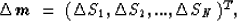 |
(3) |
where N is the total number of cells.
The second discretization I will consider will be the one based
on natural pixels (Michelena and Harris, 1991):
| 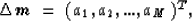 |
(4) |
where the coefficients ai are used to calculate the slowness
perturbation 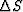 as a superposition of natural pixels
as a superposition of natural pixels 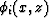
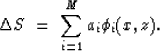
In the previous expressions, M is the total number of traveltimes, which
are calculated also along natural pixels.
Finally, I will consider the discretization of the model in homogeneous
orthogonal regions with elliptical velocity dependencies
(Michelena and Muir, 1991):
| 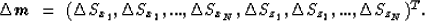 |
(5) |
The reasons why I will perform the SVD only for these three particular
parametrizations are the following:
- Compare the matrices obtained by discretizing the model
in orthogonal
homogeneous cells with those obtained by discretizing the model in
natural pixels (for the isotropic case).
- Compare the matrices obtained by allowing the model to be either
isotropic or anisotropic (when the model is discretized in
orthogonal homogeneous cells).





Next: SINGULAR VALUE DECOMPOSITION: APPLICATION
Up: Michelena: SVD
Previous: SINGULAR VALUE DECOMPOSITION: SHORT
Stanford Exploration Project
12/18/1997