




Next: FINITE DIFFERENCE METHODS
Up: NONLINEAR TRAVELTIME TOMOGRAPHY
Previous: Traveltime and slowness model
The tomographic inversion is usually done through the optimization process.
Given a slowness model, we can simulate
the wave propagation between two wells and compute the first arrival
traveltime, denoted by 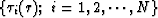 .We want to find a set of parameters
.We want to find a set of parameters 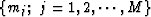 that minimizes
the differences between the traveltimes picked from the recorded data and
the traveltimes computed from the model, subjected to some linear constraints.
The mathematical description of this problem is as follows:
that minimizes
the differences between the traveltimes picked from the recorded data and
the traveltimes computed from the model, subjected to some linear constraints.
The mathematical description of this problem is as follows:
| ![\begin{displaymath}
\min_{\{m_j\}}\left\{\sum^N_{i=1}
\int_{r}\left[\tau_i({\bf m})-t_i\right]^2dr+
\Vert{\bf B}{\bf m}+{\bf c}\Vert^2\right\},\end{displaymath}](img6.gif) |
(2) |
where 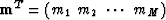 is the unknown slowness parameter
vector. Matrix
is the unknown slowness parameter
vector. Matrix 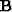 and vector
and vector  are chosen to constrain the
inversion process. Because the traveltimes are generally
nonlinear functions of the
slowness model parameters, equation (2) defines
a nonlinear optimization problem. A nonlinear optimization is usually
accomplished iteratively. In each iteration, we
linearize the traveltime functions as follows:
are chosen to constrain the
inversion process. Because the traveltimes are generally
nonlinear functions of the
slowness model parameters, equation (2) defines
a nonlinear optimization problem. A nonlinear optimization is usually
accomplished iteratively. In each iteration, we
linearize the traveltime functions as follows:
| 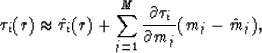 |
(3) |
where 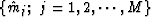 are
the slowness model parameters obtained
in the previous iteration, and
are
the slowness model parameters obtained
in the previous iteration, and 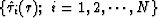 are
the traveltimes calculated from the previous model. We define
are
the traveltimes calculated from the previous model. We define
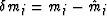 and
and 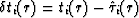 ,
and then form two vectors as follows:
,
and then form two vectors as follows:
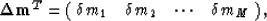
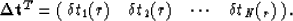
We also define 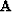 to be an
to be an 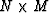 matrix with the elements
matrix with the elements
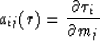
and define
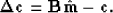
Then, equation (2) can be approximated as
| 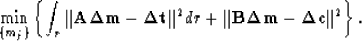 |
(4) |
Now the problem becomes a linear least squares problem. We can
use a gradient method to solve it. If we use the steepest descent
method, we need to calculate the gradient vector defined as follows:
| 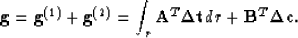 |
(5) |
This vector has a dimension of M.
If we choose the conjugate gradient method, we need to calculate,
in addition to the gradient vector,
the conjugate gradient vector defined as follows:
| 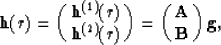 |
(6) |
which has a dimension of N plus the number of conditions.





Next: FINITE DIFFERENCE METHODS
Up: NONLINEAR TRAVELTIME TOMOGRAPHY
Previous: Traveltime and slowness model
Stanford Exploration Project
12/18/1997
![]() .We want to find a set of parameters
.We want to find a set of parameters ![]() that minimizes
the differences between the traveltimes picked from the recorded data and
the traveltimes computed from the model, subjected to some linear constraints.
The mathematical description of this problem is as follows:
that minimizes
the differences between the traveltimes picked from the recorded data and
the traveltimes computed from the model, subjected to some linear constraints.
The mathematical description of this problem is as follows:
![\begin{displaymath}
\min_{\{m_j\}}\left\{\sum^N_{i=1}
\int_{r}\left[\tau_i({\bf m})-t_i\right]^2dr+
\Vert{\bf B}{\bf m}+{\bf c}\Vert^2\right\},\end{displaymath}](img6.gif)
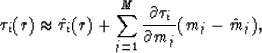
![]()
![]()
![]()
![]()