| |
(1) |
| |
(2) |
If this gather is migrated with a different velocity model ![]() , the
image obtained will be distorted from the true image of the subsurfaces.
, the
image obtained will be distorted from the true image of the subsurfaces.
| |
(3) |
Residual migration is a transformation from image ![]() to image Q(x,z). Therefore, we want to find out the relationship
between (x,z) and
to image Q(x,z). Therefore, we want to find out the relationship
between (x,z) and ![]() that defines the kinematic operators
of this transformation.
Substituting P(t,xr) from equation (1) into equation
(3) yields
that defines the kinematic operators
of this transformation.
Substituting P(t,xr) from equation (1) into equation
(3) yields
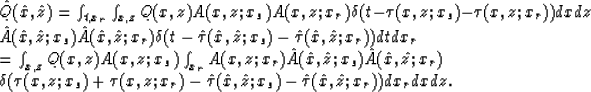 |
||
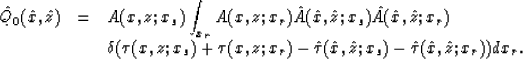 |
(4) |
It is well known that the kinematics of the summation operator that does
full migration is defined by the trajectory of the reflection event from
a scatterer.
Similarly, the kinematics of the summation operator that does residual
migration can be determined from ![]() , or more
specificly from the argument of the
, or more
specificly from the argument of the ![]() -function in equation
(4). Let
-function in equation
(4). Let
![]()
![]()
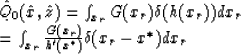 |
||
![]()
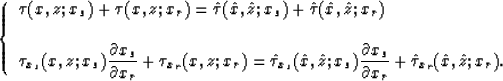 |
(5) |
![]()
![]()
For each point (x,z), equation (5) defines a curve in
![]() . This curve is exactly the kinematics of the
residual-migration operator at point (x,z).
For general velocity models, the traveltimes must be computed by
some numerical methods. These methods generate traveltime tables
rather than continuous functions. Therefore, it is
natural to solve equation (5) numerically. A straight forward
method is searching. For
each xr and (x,z), all points around (x,z) are checked to find
the
. This curve is exactly the kinematics of the
residual-migration operator at point (x,z).
For general velocity models, the traveltimes must be computed by
some numerical methods. These methods generate traveltime tables
rather than continuous functions. Therefore, it is
natural to solve equation (5) numerically. A straight forward
method is searching. For
each xr and (x,z), all points around (x,z) are checked to find
the ![]() that satisfies equation (5).
But the this algorithm is time-consuming when the dimensions
of images are large. Motivated by the results of the finite-difference
calculation of
traveltimes (Van Trier, 1990), I begin to explore the possibility to calculate
residual-migration operators with finite-difference techniques.
that satisfies equation (5).
But the this algorithm is time-consuming when the dimensions
of images are large. Motivated by the results of the finite-difference
calculation of
traveltimes (Van Trier, 1990), I begin to explore the possibility to calculate
residual-migration operators with finite-difference techniques.