Next: DISCUSSION AND CONCLUSION
Up: Claerbout: Extending a CMP
Previous: MOVIE OF NONSTATIONARITY
The velocity transform 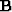 comes close to an invertible operator
because Radon transforms are theoretically invertible.
The velocity transform is a Radon transform with hyperbolic distortion.
I think the main invertibility problem
stems from numerical approximations in my definition of
comes close to an invertible operator
because Radon transforms are theoretically invertible.
The velocity transform is a Radon transform with hyperbolic distortion.
I think the main invertibility problem
stems from numerical approximations in my definition of 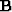 .Unlike
.Unlike 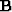 , operators more typically found
in inversion formulations like (2)
are both overdetermined and unconstrained.
In consequence,
I believe we can regard the missing data
as the free variables instead of regarding
the velocity space
, operators more typically found
in inversion formulations like (2)
are both overdetermined and unconstrained.
In consequence,
I believe we can regard the missing data
as the free variables instead of regarding
the velocity space 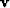 as the free variables.
I'd like to regard the transformation of the complete data space
as the free variables.
I'd like to regard the transformation of the complete data space  to the velocity space
to the velocity space 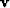 as nearly unitary and noiseless
by comparison to that transformation with the truncated data space.
Thus in the formulation (2),
the first term could be identically zero.
Whether this is valid,
it is my presumption for the rest of this paper.
I presume the problem to be solved is the minimization
of the right-hand term in (2).
(As we'll see the validity of this assumption
is not supported by the field-data trials.)
as nearly unitary and noiseless
by comparison to that transformation with the truncated data space.
Thus in the formulation (2),
the first term could be identically zero.
Whether this is valid,
it is my presumption for the rest of this paper.
I presume the problem to be solved is the minimization
of the right-hand term in (2).
(As we'll see the validity of this assumption
is not supported by the field-data trials.)
Happiness is noticing that a problem is much simpler
than you had expected.
I suddenly realized that the heart of the problem is contained
in a much smaller operator than I had thought.
Notice that it is computationally easy
to decompose integral operators into parts, in this case,
into the part of known data and missing data.
That is to say, velocity space is
The big operator is the one involving the known data 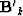 and the little operator is the one involving the few missing
traces we will add at the end of the gather
and the little operator is the one involving the few missing
traces we will add at the end of the gather 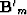 .Both transform to the same plane in velocity space.
Thus the regression
.Both transform to the same plane in velocity space.
Thus the regression
| 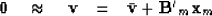 |
(7) |
involves the ``small'' operator and because it is small,
it is reasonable to use many iterations
if that should turn out to be helpful.
The idea of minimizing power in image space (velocity space)
may be questionable,
but makes more intuitive sense when you include a weighting function.
Ideally the weighting function would be the inverse of the envelope
of the expectation of the variance of the velocity space.
In practice we don't know what that is, so I used the envelope
of the first estimated velocity space, i.e. that determined
from zero padded data.
As is common practice I smoothed the envelope and added a constant
and experimented with various sized constants.
In practice it happened that few iterations were needed.
Convergence appeared to happen on the first iteration.
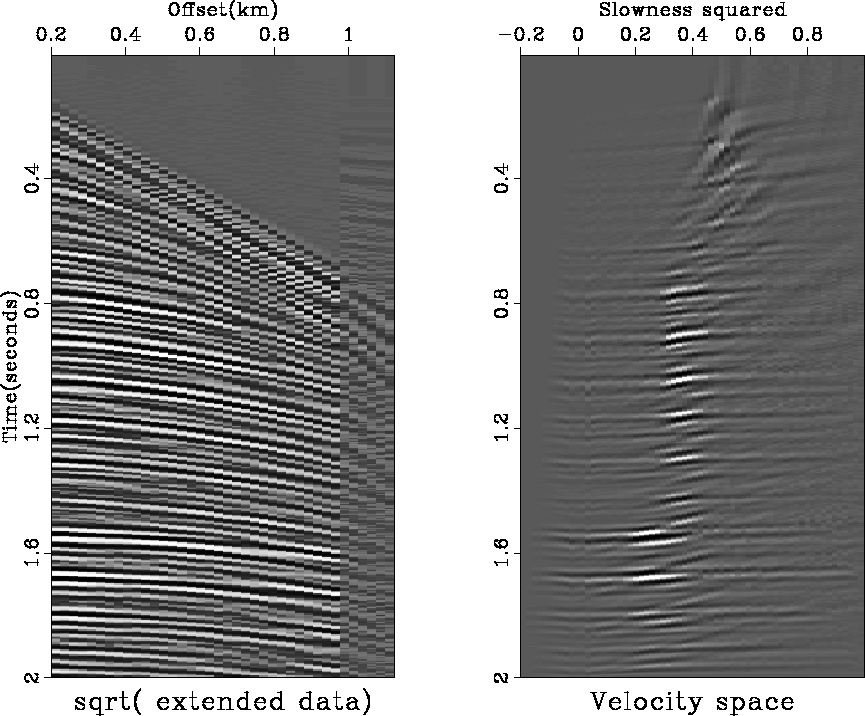
myplot
Figure 1
Attempt to extrapolate a data set.






Next: DISCUSSION AND CONCLUSION
Up: Claerbout: Extending a CMP
Previous: MOVIE OF NONSTATIONARITY
Stanford Exploration Project
1/13/1998