




Next: MOVIE OF NONSTATIONARITY
Up: Claerbout: Extending a CMP
Previous: INTRODUCTION
Let  denote a data plane in time and offset.
Let
denote a data plane in time and offset.
Let 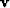 denote a model plane in velocity and vertical time.
Let
denote a model plane in velocity and vertical time.
Let 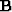 denote a modeling program.
In this study I chose
denote a modeling program.
In this study I chose 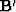 to be the pixel-precise data processing operator
(Claerbout [Pixel..., 1990]).
Thus the modeling operator is defined
to be the transpose conjugate of a well-known processing operator.
To a wave theorist this may seem strange,
but the goal is to learn how to best handle truncation and
aliasing so any reasonable approximation
to the kinematics should be fine.
to be the pixel-precise data processing operator
(Claerbout [Pixel..., 1990]).
Thus the modeling operator is defined
to be the transpose conjugate of a well-known processing operator.
To a wave theorist this may seem strange,
but the goal is to learn how to best handle truncation and
aliasing so any reasonable approximation
to the kinematics should be fine.
Linear inverse theory suggests an algorithm based on
| ![\begin{displaymath}
\min_v \quad[ ({\bf x}- {\bf B}\v)'\bold W_{xx}({\bf x}- {\bf B}\v) +
\lambda \v ' \bold W_{vv} \v
]\end{displaymath}](img5.gif) |
(1) |
where 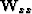 and
and 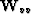 are the usual inverse covariance
weighting functions and
are the usual inverse covariance
weighting functions and 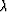 is a parameter
that is presumably explained by the textbook literature
(though SEP-65 page 214 shows some pitfalls there.)
We'll consider weights later.
For the unweighted problem the formal solution is a power series in
is a parameter
that is presumably explained by the textbook literature
(though SEP-65 page 214 shows some pitfalls there.)
We'll consider weights later.
For the unweighted problem the formal solution is a power series in 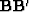 .In real life, the operator
.In real life, the operator 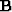 is expensive,
especially considering the huge volume of data requiring analysis.
I chose to consider only the first two terms of the power series
for careful examination to identify the most significant practical effect,
is expensive,
especially considering the huge volume of data requiring analysis.
I chose to consider only the first two terms of the power series
for careful examination to identify the most significant practical effect,
| 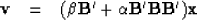 |
(2) |
where  and
and 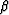 have yet to be chosen.
In the formula (2) the data is taken
to be separable into two parts,
the known k and the missing m which is taken to be zero, say
have yet to be chosen.
In the formula (2) the data is taken
to be separable into two parts,
the known k and the missing m which is taken to be zero, say
| 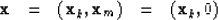 |
(3) |





Next: MOVIE OF NONSTATIONARITY
Up: Claerbout: Extending a CMP
Previous: INTRODUCTION
Stanford Exploration Project
1/13/1998