HOLOGRAPHY

The volume integral representation of the Porter-Bojarski integral allows the backpropagation of the homogeneous portion in the measured data. We can not backpropagate the inhomogeneous portion. Nevertheless, if the inhomogeneous waves are weak in amplitude compared to the homogeneous waves, we can get a good subsurface image. Although we didn't use any weak scatterer approximation for the derivation of the Porter-Bojarski integral, the image obtained from the integral will not be complete if there are strong scatterers near our geophones. The seismic exploration industry solves this problem by cutting off evanescent energy and being content with the homogeneous wave image. It is more clever to continue downward the homogeneous waves to a certain reflector, let the reflector explode, and use the difference of synthetic and registered data to guess the evanescent energy and to update the reflection coefficients. This can be done iteratively.

Programming the Porter-Bojarski integral for the backpropagation from an arbitrary surface S leads to an algorithm called generalized holography. It performs the backpropagation of homogeneous waves with a constant frequency.

 

Figure 1: Derivation of the Raleigh integrals.

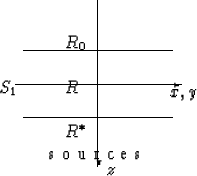
Let us for a moment consider the Kirchhoff integral for the special case of a planar registration surface S₁. We assume Cartesian coordinates and some scatterers only in the lower halfspace. We construct a halfsphere S=S₁ + S₂ in the upper halfspace with the x-y-plane being the registration plane. If the radius approaches infinity, we can ignore the energy scattered through the part of the halfsphere with $z \neq 0$ but not through the registration plane. Remember that the Kirchhoff integral is zero if we march from S₁ towards the sources. Now subtract the wavefields from a plane slightly above and parallel to S₁ in a distance R₀ and a plane very close but below S₁ in a distance R^* and also parallel to the observation plane

$$\begin{eqnarray} p(R,\omega) = \oint_{S_{1}} & [ p(R_0,\omega) ({\frac{\partial}... ...e {n}}}}p(R_0,\omega) (G(R-R^*,\omega)-G(R-R_0,\omega))] dS \ \ . \end{eqnarray}$$ (11)

Close to S₁ both Green's functions are identical. The normal derivatives differ only in their sign. Therefore, we simplify the Kirchhoff integral to obtain the Raleigh II integral

$$2 \oint_{S_{1}} [p(R_0,\omega) {\frac{\partial}{\partial{z}}}G(R-R_0,\omega)] dS = p(R,\omega) \ \ .$$ (12)

The Raleigh II integral allows forward propagation by the superposition of monopoles $p(R_0,\omega)$ along the plane z=0.

If we add the integrals for above and below the observation plane, we get the Raleigh I integral

$$2 \oint_{S_{1}} [ {\frac{\partial}{\partial{z}}}p(R_0,\omega) G(R-R_0,\omega)] dS = p(R,\omega) \ \ .$$ (13)

It says: superpose all dipoles ${\frac{\partial}{\partial{z}}}p(R_0,\omega)$ on S₁ and obtain the wave field $p(R,\omega)$ via forward propagation.

Equivalent Raleigh formulations for the Porter-Bojarski integral are obtained by inserting the conjugate complex Green's functions G^*. If we consider the registration surface of reflection seismic surveys to be a plane, it will be sufficient to backpropagate only monopoles with a Raleigh II type representation of the Porter-Bojarski integral. We don't have to know the gradient of the wavefield. This shouldn't be news for you, but the explanations given for this fact by Schneider (1978) and others are rather heuristical.

Programming the Raleigh I or Raleigh II integrals leads to the so-called Raleigh Sommerfeld Holography (Langenberg, K.L., 1986). It performs the backpropagation of homogeneous waves emitted by dipoles or monopoles for constant frequencies.

 

Figure 2: Cut through the Ewald sphere $\Gamma (k_i)$. The object function $\Gamma (k)$ is shifted by the incident wave k_i and intersects with the Ewald sphere.

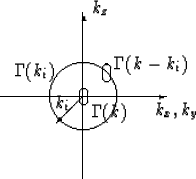Until now we always considered holography in the $\omega-R-$space. Let us study our problem in the frequency wavenumber domain. A homogeneous plane wave is in the k-space located on the Ewald sphere (Ashcroft, N.W., Mermin, N.D., 1981).The Ewald sphere is a sphere in the Cartesian k-space with the radius

$$\vert k_i\vert = \frac {\omega}{v} = \sqrt{{k_x}^2 +{k_y}^2+{k_z}^2} \ \ .$$ (14)

where k_i = (k_x,k_y,k_z) determines the direction $\frac {k_i}{\vert k_i\vert}$ and frequency $\omega = \vert k_i\vert v$of the incident wave in a medium of constant velocity v. Suppose we want to image an object function $\Gamma (k)$ with an incident wave defined by k_i. The object function may describe a velocity heterogenity of the medium. On the observation plane we measure an object function shifted in space $\Gamma (k-k_i)$. To be more precise: for a given angle of incidence and a given frequency, we measure the intersection of the shifted object function and the Ewald sphere. Backpropagation means shifting the intersection back, i.e., to undo the space shift due to the wavepath.

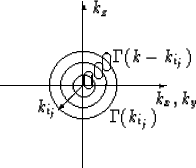
To image we have to superpose as many intersections of Ewald spheres and object functions as possible to get a high resolution. There are basically two possibilities to get different intersections

1.

frequency diversity

2.

angular diversity .

Frequency diversity varies the frequency $\omega$ and doesn't change the angle of incidence. Each frequency defines a new Ewald sphere so that different intersections with the object function will have different curvatures. Angular diversity changes the angle of incidence but holds the frequency constant. If the angular coverage is large enough, we can cover one whole Ewald sphere. Bandpassed records are located within a circular ring and limit the spatial resolution as a poor angular coverage does, i.e., if only parts of the Ewald sphere are covered.

 

Figure 3: Frequency diversity. The shifted object function $\Gamma (k-k_{i_{j}})$ intersects with different Ewald spheres $\Gamma (k_{i_{j}})$.

 

Figure 4: Angular diversity. The shifted object function $\Gamma (k-k_{i_{j}})$ intersects with the same Ewald sphere at different angles.

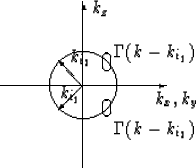Superposition of all possible backshifted intersections, i.e., a complete coverage of the k-space, yields to an ``optimal'' image with homogeneous waves. But we still miss the information of inhomogeneous waves due to strong scatterers or sources near the geophones.

Doing generalized holography or Raleigh Sommerfeld Holography for different frequencies leads to the frequency diversity filtered backpropagation algorithm:

• measure the intersection of the Ewald sphere with the shifted object function for different frequencies but constant incidence angle
• make a temporal deconvolution
• shift the Ewald sphere intersections back to the origin (backpropagation)
• superpose the images for different frequencies
• superpose the backpropagated and incident wavefields

The angular diversity generalized filtered backpropagation algorithm is similar:

• measure the cut of the Ewald sphere with $\Gamma (k-k_i)$for different angles of incidence but for the same frequency. (We apply a lowpass because the intersections are within the sphere 2|k_i|.)
• shift the Ewald sphere intersections back to the origin (backpropagation)
• superpose the images for different angles
• superpose the backpropagated and incident wavefields

Either frequency diversity or angular diversity can image the object if we have a complete coverage of the k-space. In practice, our data is bandpassed and registration on a plane limits the angular resolution. The seismic processing will be more sucessful if we can combine all the information we have. Prestack migration yields to better results than Zero-offset migration because the bandpassed frequency diversity of Zero-offset migration is completed by a limited angular diversity.

If our data is recorded on a plane, we should speak of the Raleigh Sommerfeld frequency diversity or angular diversity algorithms. For a constant velocity medium, Raleigh Sommerfeld angular diversity holography is nearly the same as diffraction tomography that will be studied in the next section.