The basis of the iterative methods is the non-iterative ``deterministic'' approach to seismic inversion. It ignores the random components of seismic data and is strictly speaking less deterministic than the iterative inversion. The reason it is sometimes considered as deterministic is that it is based on the forward scattering problem that can be solved exactly by the Kirchhoff integral. People took the forward solutions and simply changed the direction of the wave propagation. The resultant integrals converge only between finite integration limits that cut off evanescent energy. Therefore, this method constructs images by backpropagating only the homogeneous part of the registered wavefield. Iterative methods treat evanescent energy at least statistically so that they should lead to more accurate images.
For didactical reasons we will now consider the Kirchhoff integral in its simplest form: for an homogeneous acoustic medium. The following concepts can be extended to inhomogeneous elastic media.
The Kirchhoff integral takes a wavefield ![]() and its normal
derivative
and its normal
derivative ![]() measured on an arbitrary
closed surface S surrounding the sources and propagates
the field forward, away from the sources to an arbitrary place R0
outside the surface. The normal vector
measured on an arbitrary
closed surface S surrounding the sources and propagates
the field forward, away from the sources to an arbitrary place R0
outside the surface. The normal vector ![]() points to the outside
of V that is away from the sources.
The volume V is enclosed by S and contains the source volume VS.
Inside of V the Kirchhoff integral
is zero. A Green's function
points to the outside
of V that is away from the sources.
The volume V is enclosed by S and contains the source volume VS.
Inside of V the Kirchhoff integral
is zero. A Green's function ![]() extrapolates the
registered wave field from R to R0.
extrapolates the
registered wave field from R to R0.
If R0 is inside of V we have:
| (2) |
| (3) |
The physical interpretation of the Kirchhoff integral is that of a forward
propagation and superposition
of Huygen's sources on S. We assume two kinds of sources: monopoles
![]() and dipoles
and dipoles ![]() . In case of stiff boundary conditions
(von Neumann conditions) on S, we can drop the term
. In case of stiff boundary conditions
(von Neumann conditions) on S, we can drop the term
![]() and for a weak boundary S only the gradient
and for a weak boundary S only the gradient
![]() is of importance and we drop the term containing
is of importance and we drop the term containing
![]() (Dirichlet boundary condition).
(Dirichlet boundary condition).
So far we learned how to forward propagation. For backpropagation, i.e. if we propagate towards the sources, the Kirchhoff integral has to be modified. Two changes have to be made:
| (4) |
G and G* solve the inhomogeneous wave equation for a point source:
| (5) |
| (6) |
| (7) |
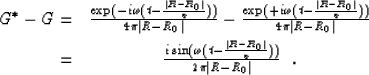 |
||
| (8) |
| (9) |
The homogeneous wavefield is used in standard seismic
imaging
where we have to superpose
the forward extrapolated wavefield and the backward extrapolated waves
to get a representation of the subsurface by
homogeneous waves at the time they were scattered from a discontinuity.
Usually we propagate
with the same sign of ![]() for both forward and
backward propagating Green's functions.
This explains why we subtracted the forward and backward extrapolated
waves, whereas in prestack migration, they have to be added.
for both forward and
backward propagating Green's functions.
This explains why we subtracted the forward and backward extrapolated
waves, whereas in prestack migration, they have to be added.
The surface integral of Porter and Bojarski also has a volume integral representation
| (10) |