10: EXTREMAL VELOCITIES

We know how to determine the image of a reflector's location on a migrated section. This location, of course, depends on the choice of the continuation velocity v_c. Being independent of a weight function $w({\bf r},r)$, the location of caustics in the x,z-plane is determined by the system of equations  

$${\partial T(x,z,r) \over {\partial r}} - {{d \tau_0}\over {dr}} = 0$$ (102)

and  

$${\partial ^2 T(x,z,r) \over {\partial r^2}} - {{d^2 \tau_0}\over {dr^2}} = 0.$$ (103)

If at some velocity v_c = v_ex the caustic and the image cross each other at a special point ${\bf r}$, we call this the extremal velocity v_ex. Usually we have a continuous interval of extremal velocities: $v_{ex} \in V_{ex}$.Typically for each $v_{ex} \in V_{ex}$ one can observe two or more special points. For some value v_ex = v^*_ex called the true extremal velocity, these special points unify in one point that appears as a bright spot.

Example: If the true model represents a homogeneous medium with velocity v and a planar reflector at depth h, the location of the reflector's image after CSP-migration is described by the system of equations (see Chapter 7):

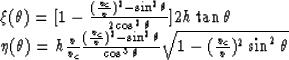To find the location of caustics, we substitute $\tau_0(r) = {1 \over v} \sqrt{r^2 + 4 h^2}$ and $T(x,z,r)={1 \over v_c} \sqrt{(r-x)^2 + z^2}$.into system equations (102) and (103). So we have the system of equations

If for some $\theta$ and r we have $\xi = x$ and $\eta = z$, then the reflector's image contains the special point $(\xi ,\eta)$.Calculations show that at v_c < v there is no special point on the image. At $v < v_c < \sqrt{2}$ we have two symmetrical special points which merge together into the one bright point when $v_c = \sqrt{2} v \equiv v_{ex}^*$ (as shown in Figure ).

Instead of a complete investigation of the situation, we can choose some particular ray of the eikonal $\tau^{(-)}$.It is not difficult to determine the meaning of ${\partial ^2T({\bf r},r)} \over {\partial r^2}$ for the given velocity v=v_c and the point ${\bf r}^{\prime}$ belonging to the image and the ray $\gamma$; we can easily check condition (103). Let us again consider CSP-migration with the true model containing a curved reflector in a homogeneous medium (Figure , solid line). Let us choose the ray $\gamma_s$ which approaches the surface $\Sigma$ vertically. This ray is connected with a stationary point r_s of the function $\tau_0(r)$:

$${d\tau_0 \over {dr}}\vert _{r=r_s} = 0$$

and we shall call this ray stationary. We shall denote h the true depth of the reflector and h_m the image depth for the x=r_s. If $\tau_0(r_s)=t_s$, then h_m satisfies  

$${h_m \over v_c} + {\sqrt{h_m^2 + r_s^2} \over v_c} = t_s .$$ (104)

It is easy to show that  

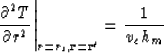$$\left.{{\partial ^2 T} \over {\partial r^2}} \right\vert _{r=r_s,{\bf r}={\bf r}^{\prime}} = {1 \over {v_c h_m}}$$ (105)

The point ${\bf r}^{\prime} = (r_s,h_m)$ belongs to a caustic if  

$${1 \over {v_c h_m}} = {{d^2 \tau_0} \over {dr^2}} \vert _{r=r_s}$$ (106)

Using equation (104), we have  

$$h_m = {{t_s^2 v_c^2 - r_s^2} \over {2 t_s v_c}}.$$ (107)

Combining (106) and (107) we receive  

$$v_c = v_{ex} = \sqrt{ {2 \over {t_s {{d^2 \tau_0} \over {dr^2}}} } + ({r_s \over t_s})^2}$$ (108)

It is easy to derive (see Figure )  

$$r_s = h \tan(2 \phi) , \qquad t_s = {{2 \cos^2 \phi} \over {\cos(2 \phi)}}{h_m \over v_c} .$$ (109)

As for ${d^2 \tau_0} \over {dr^2}$ we can use standard techniques based on the continuation of wave front curvatures along the ray. We shall omit all these calculations and give the final result:  

$${{d^2 \tau_0} \over {dr^2}} \vert _{r=r'} = {1 \over {v h}} ... ...cos \phi~\cos(2 \phi) + 2 k h} \over { 2 ( \cos^3 \phi + k h)}}$$ (110)

where k is the reflector curvature at point ${\bf r}$. Substitution of equations (109) and (110) into (108) gives  

$$v_{ex} = {{\sqrt{2} v} \over {\cos \phi}} \sqrt{ {{\cos (2 \... ... {\cos \phi~\cos (2 \phi) + 2 k h}} + {1 \over 2} \sin^2 \phi }$$ (111)

If the reflector is planar (k=0), then  

$$v_{ex} = v {\sqrt{1+\cos^2 \phi} \over {\cos \phi}}$$ (112)

If the point ${\bf r}^{\prime}$ is stationary for the reflector ($\phi = 0$), then  

$$v_{ex} = \sqrt{2} v {\sqrt{{1 + k h} \over { 1+ 2k h}}}$$ (113)

If the reflector is planar and horizontal (k=0 and $\phi = 0$), then  

$$v_{ex} = \sqrt{2} v$$ (114)

and, at last, if we have a point reflector ($k=\infty$), then

 

v_ex = v (115)

Is this velocity v_ex the true extremal velocity? It is in all particular situations expressed by formulas (112) - (115).

In the zero offset case for arbitrary rays

$$v_{ex} = v \sqrt{ {1 + k h \cos \phi} \over {1 + k h \cos \phi~\sin^2 \phi}}$$

and at $\phi = 0$

$$v_{ex} = v \sqrt{1 + {1 \over {kh}}}$$

If k=0 (planar reflector) we formally receive $v_{ex}=\infty$, but in this case the amplitude does not actually depend on the meaning of the velocity v_c.

In the common mid-point case travel-time curves for a point reflector and for a flat reflector are the same. It means that in this situation v_ex=v.