B. Two-layer media

Let the first layer with horizontal bedding z=h₁ have the velocity v₁, and the second layer with the dipping bed

$$z=h_{1}+h_{2}+x\tan \phi$$

have velocity v₂. Time-migration is performed in homogeneous model with velocity $v_{c}={v^{\prime} \over 2}$.

First step:

$$t_{0} (x)= {2h_{2} \cos \phi \over v_{2}} + {2h_{1} \over v_... ...over v_{2}})}^{2} \sin^{2} \phi} + {2 \sin \phi \over v_{2}} x.$$

Second step: $(v_{c}={v^{\prime} \over 2})$ :

$$\tau ^{(-)}(x,z)= {2h_{2} \cos \phi \over v_{2}} + {2 h_{1} ... ...e}} \sqrt{1 - {({v^{\prime} \over v_{2}})}^{2} \sin^{2} \phi }.$$

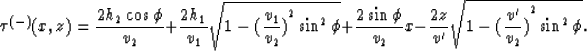
Third step: imaging (from the condition (74)):

$$z={({v^{\prime}\over v_2}) \cos \phi \over \sqrt{1 - {({v^{... ...i } \over ({v_{1}\over v_{2}})\cos \phi } + x \tan \phi \right]$$

After substitution $z=v^{\prime}t$, we obtain location of reflector image in the time section:  

$$t={\cos \phi \over v_{2} \sqrt{1 - {({v^{\prime} \over v_{2... ...} \over ({v_{1}\over v_{2}})\cos \phi } + x \tan \phi \right].$$ (75)

Let us perform time-to-depth migration in true two-layer model with the help of Hubral's technique (Hubral, 1977). This technique consists of transmission of amplitudes along image rays, which satisfy Snell's law and approach the surface $\Sigma$ vertically. But in this simple example all image rays are vertical in both layers. So the location of the reflector's image in depth-section will be derived from the equation:

$$t - {h_{1}\over v_{1}} - {(z-h_{1})\over v_{2}}=0$$

where t must be expressed according to equation (75). After simple manipulation we derive

$$z={\cos \phi \over \sqrt{1 - {({v^{\prime} \over v_{2}})}^{... ...\phi \right] -h_{1} \cdot \left( {v_{2} \over v_{1}} -1 \right)$$

that differs from true position of the reflector.