Exercise:     ($\omega$,x,z)-Wavefield Extrapolation

This document is an actual exercise taken out of Jon Claerbout's book Imaging the Earth's Interior. This exercise performs a wavefield extrapolation in ($\omega$,x,z)-space. At the top boundary data are given as if recorded from a spherically diverging wave coming from within the medium. The goal of this exercise is to show that the ($\omega$,x,z)-space can be used for downward extrapolation of recorded data. The following is a listing of the existing program written in ratfor. It is directly included from the directory in which this document is stored.

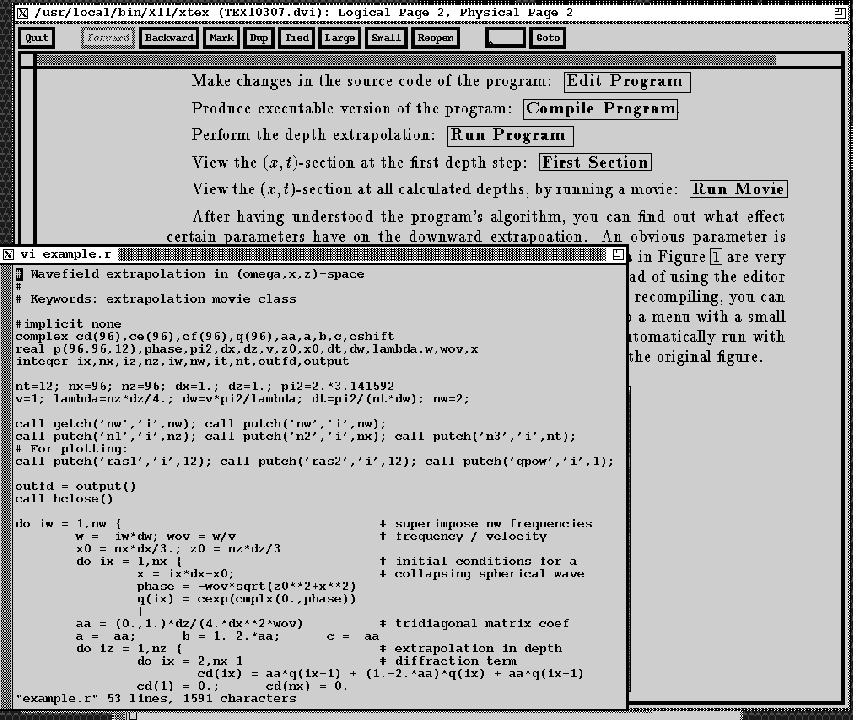
# Wavefield extrapolation in (omega,x,z)-space
#
# Keywords: extrapolation movie class
#implicit none
complex cd(96),ce(96),cf(96),q(96),aa,a,b,c,cshift
real p(96,96,12),phase,pi2,dx,dz,v,z0,x0,dt,dw,lambda,w,wov,x
integer ix,nx,iz,nz,iw,nw,it,nt,outfd,output

nt=12; nx=96; nz=96; dx=1.; dz=1.; pi2=2.*3.141592
v=1; lambda=nz*dz/4.; dw=v*pi2/lambda; dt=pi2/(nt*dw); nw=2;

call getch('nw','i',nw); call putch('nw','i',nw);
call putch('n1','i',nz); call putch('n2','i',nx); call putch('n3','i',nt);
# For plotting:
call putch('ras1','i',12); call putch('ras2','i',12); call putch('gpow','i',1);

outfd = output()
call hclose()

do iw = 1,nw {					# superimpose nw frequencies
	w =  iw*dw; wov = w/v			# frequency / velocity
	x0 = nx*dx/3.; z0 = nz*dz/3
	do ix = 1,nx {				# initial conditions for a
		x = ix*dx-x0;			# collapsing spherical wave
		phase = -wov*sqrt(z0**2+x**2)
		q(ix) = cexp(cmplx(0.,phase))
		}
	aa = (0.,1.)*dz/(4.*dx**2*wov) 		# tridiagonal matrix coef
	a = -aa;      b = 1.+2.*aa;      c = -aa
	do iz = 1,nz {				# extrapolation in depth
		do ix = 2,nx-1			# diffraction term
			cd(ix) = aa*q(ix+1) + (1.-2.*aa)*q(ix) + aa*q(ix-1)
		cd(1) = 0.;      cd(nx) = 0.
		call ctris(nx,-a,a,b,c,-c,cd,q,ce,cf)
			# Solves complex tridiagonal equations
		cshift = cexp(cmplx(0.,wov*dz))
		do ix = 1,nx			# shifting term
			q(ix) = q(ix) * cshift
		do it=1,nt {			# evolution in time
			cshift = cexp(cmplx(0.,-w*it*dt))
			do ix = 1,nx
				p(iz,ix,it) = p(iz,ix,it)+q(ix)*cshift
			}
		}
	}
do it=1,nt
	do ix=1,nx
		call rite(outfd, p(1,ix,it), nz*4)
call exit(0)
stop;		end

You are encouraged to make your own versions of this program by editing the file. Here are a few actions provided for you. To carry out the command, press the middle mouse button in the appropriate box:

Make changes in the source code of the program: Edit Program .sepsh>make Edit Program

cake edit_example

Produce executable version of the program: Compile Program.sepsh>make Compile Program

cake compile_example

Perform the depth extrapolation: Run Program .sepsh>make Run Program

cake run_example

View the (x,t)-section at the first depth step: First Section.sepsh>make First Section

cake first_example

View the (x,t)-section at all calculated depths, by running a movie:

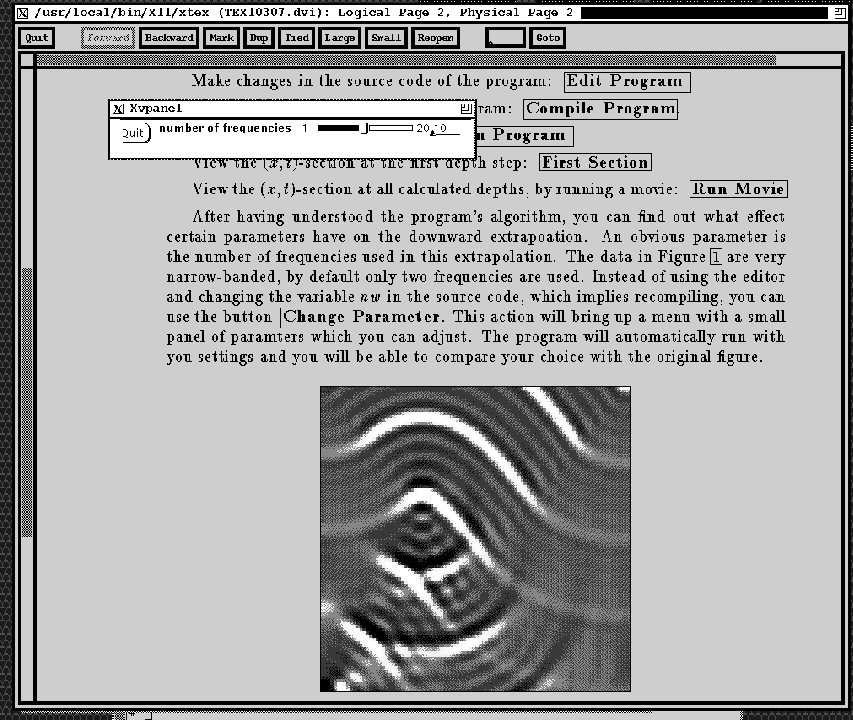
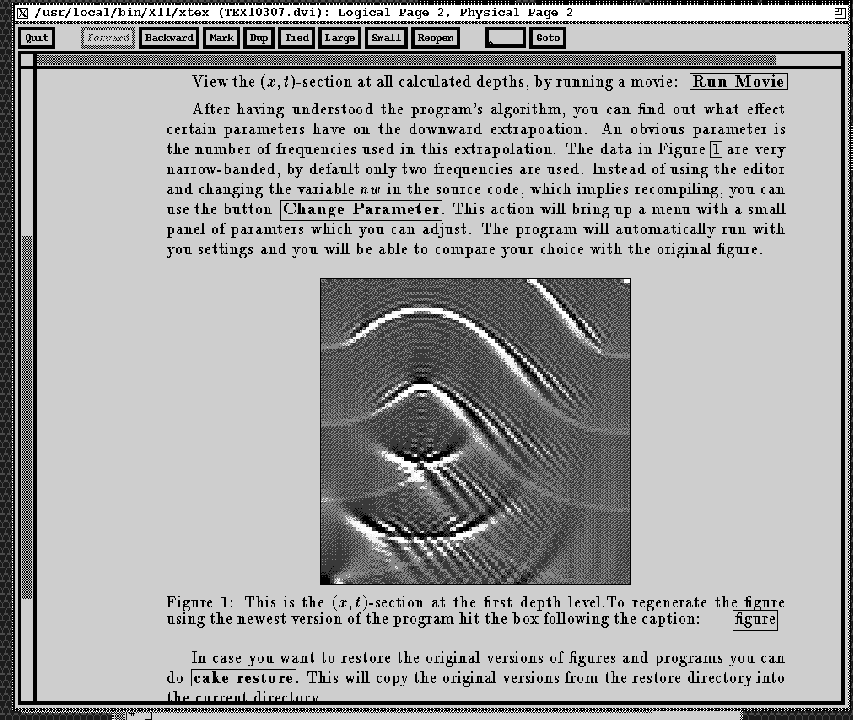
After having understood the program's algorithm, you can find out what effect certain parameters have on the downward extrapolation. An obvious parameter is the number of frequencies used in this extrapolation. The data in Figure 1 are very narrow-banded, by default only two frequencies are used. Instead of using the editor and changing the variable nw in the source code, which implies recompiling, you can use the button . This action will bring up a menu with a small panel of parameters which you can adjust. The program will automatically run with you settings and you will be able to compare your choice with the original figure.

 

figure
Figure 1 This is the (x,t)-section at the first depth level. To regenerate the figure using the newest version of the program hit the box following the caption:

In case you want to restore the original versions of figures and programs you can do . This will copy the original versions from the restore directory into the current directory.

 

dump1
Figure 2 This figure shows the xtex previewer in use. Only the basic text and figures are visible on this screen. Note the presence of several buttons on the screen.

 

dump2
Figure 3 When the Edit Program button is pressed a window appears on the screen to allow the user to edit the ratfor program. After the editing session is complete the user can compile the program by pressing the Compile Program button. Note that actually the Compile Program and Run Program buttons are redundant. The dependencies specified in the Cakefile will ensure that the program is recompiled and rerun if necessary. The buttons are included so that the user can run each action in isolation for testing purposes.

 

dump3
Figure 4 When the program has been successfully compiled the user can run the program to create a synthetic dataset by pressing the Run Program button. The user can the see the results by pressing either the First Section or Run Movie button. In this example the Run Movie button has been pressed and the user has a movie of the data visible on the screen.

 

dump4
Figure 5 Another possible method of interaction is to run a command that prompts the user for a processing parameter. If the Change Parameter button is pressed the Xvpanel program described by Steve Cole in this report is invoked. It has been set up to prompt the user for the number of frequencies to use in the modeling. The user has chosen ten frequencies in this example.

 

dump5
Figure 6 The user can press the figure button in the plot caption to view the new version of the figure. Note that because the dependencies in the Cakefile include the parameter file modified in the previous example the program is rerun using the new parameter, ten frequencies instead of the default of two. The changes are clearly visible.