|
|
|
|
Two point raytracing for reflection off a 3D plane |
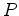 -to-
-to-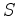 or
or 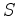 -to-
-to-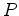 reflection as well with
one important difference--the angle of reflection differs from the
angle of incidence. Now
reflection as well with
one important difference--the angle of reflection differs from the
angle of incidence. Now
for some scalar
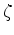 . To determined
. To determined 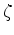 let
let 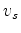 and
and 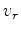 be the velocities of the source and receiver paths
respectively and
be the velocities of the source and receiver paths
respectively and 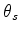 and
and 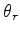 be the corresponding
angles of incidence and reflection. Then Snell's Law says
be the corresponding
angles of incidence and reflection. Then Snell's Law says
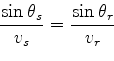 .
.
By our definition of
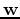 , we also have the identities
, we also have the identities
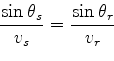
which, using the identity,
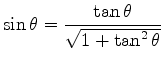 ,
,
gives the relation for
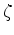
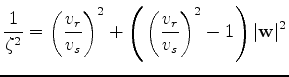
which, combined with
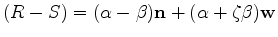 ,
,
produces a fourth order equation for
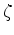 .
.
The fourth order equation can be solved directly using algebraic formulas. Lanczos (1956) provides a clean, efficient numerical approximation, reproduced in Appendix A, that is about 10 times faster than using a general purpose numerical root finder. (Appendix B shows how to make it free of floating point divisions.)
An interesting alternative to direct solution is to apply Newton iterations to the shooting method wherein source ray parameters are repeatedly adjusted to return very near to the target receiver. This approach applies to multiple layers and multiple reflections, not just a single interface. In Appendix C, I demonstrate global convergence of that method when applied to forward ray tracing through a stack of horizontal layers.
|
|
|
|
Two point raytracing for reflection off a 3D plane |