|
|
|
|
Fast log-decon with a quasi-Newton solver |
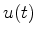 .
Claerbout shows that the gradient
.
Claerbout shows that the gradient 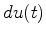 of the sparse log-decon method
corresponds to the crosscorrelation of the residual (the reflectivity series)
with the soft-clipped residual (see Claerbout et al. (2012) for
a generalization with a variable gain). The pseudo-code below
shows the steepest descent algorithm.
of the sparse log-decon method
corresponds to the crosscorrelation of the residual (the reflectivity series)
with the soft-clipped residual (see Claerbout et al. (2012) for
a generalization with a variable gain). The pseudo-code below
shows the steepest descent algorithm.
Once 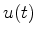 is estimated, we obtain the wavelet
is estimated, we obtain the wavelet
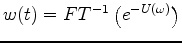 and the sparse
decon output
and the sparse
decon output
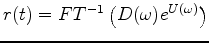 , where
, where 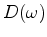 is the Fourier transformed
input data.
is the Fourier transformed
input data.