|
|
|
|
P/S separation of OBS data by inversion in a homogeneous medium |
The isotropic elastic wave equation relates displacements to stresses via two elastic constants - the Lam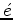 parameters
parameters 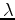 and
and 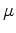 :
:
where 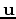 are the particle displacements in each dimension,
are the particle displacements in each dimension, 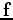 is the force function and
is the force function and 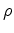 is medium density. An alternate formulation is:
is medium density. An alternate formulation is:
From equation 10, the explicit form for a heterogeneous two dimensional medium can be expressed in a matrix-vector notation as:
The forward elastic propagation operator can then be expressed as:
For a homogeneous medium, and using a Green's function to describe the energy propagation between any two locations
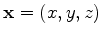 and
and
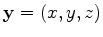 , the equation takes the form:
, the equation takes the form:
The forward elastic propagation operator injects sources from a model into some location in the medium, and records the resulting wavefield at some other location:
where 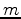 is the model of injected sources at location
is the model of injected sources at location 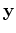 in the medium, and
in the medium, and 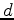 are the recorded displacement fields
are the recorded displacement fields 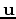 at location
at location 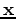 in the medium.
in the medium. 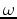 is angular frequency and
is angular frequency and
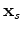 is the shot gather. In vector notation, this is expressed as
is the shot gather. In vector notation, this is expressed as
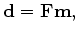 |
(15) |
where 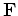 is the forward operator. The adjoint operator injects the data from the same recording locations, and records the resulting wavefield at the model injection points:
is the forward operator. The adjoint operator injects the data from the same recording locations, and records the resulting wavefield at the model injection points:
which in vector notation is
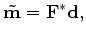 |
(17) |
where
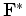 is the adjoint operator.
is the adjoint operator.
|
|
|
|
P/S separation of OBS data by inversion in a homogeneous medium |