Identifying reservoir depletion patterns from production-induced deformations with applications to seismic imaging

Heterogeneous Models

Although the asymptotic technique discussed in an earlier section addresses to some extent the issue of inhomogeneous models, it is inherently limited to moderate heterogeneity. However, practical applications of this method would require a more accurate handling of heterogeneity. Because layered models are of particularly high importance due to their commonality, we first consider modeling displacements for a vertically heterogeneous and horizontally slowly-varying medium. Rather than trying to solve a heterogeneous analogue of system 1 and 2, we will assume that one or all components of the displacement at a fixed depth 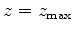$z=z_{\textrm{max}}$ immediately above the reservoir are known a priori. For example, we may use operator 5 to model displacements near the reservoir where the effect of the spatial heterogeneity of elastic parameters is limited. With displacements at 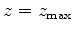$z=z_{\textrm{max}}$ and free-surface boundary conditions at 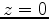$z=0$ , the problem of modeling subsurface displacements is reduced to solving a boundary-value problem for the elastostatic system:

$$\mu\left(\frac{\partial u_i}{\partial x_j}+ \frac{\partial u_j}{\... ...i}\right)+\frac{2 \mu \nu}{1-2\nu}\frac{\partial u_k}{\partial x_k}\delta_{ij}= \sigma_{ij},$$

$$\frac{\partial \sigma_{ij}}{\partial x_j}= 0,$$ (14)

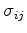where indices run from 1 to 3, $\sigma_{ij}$ denote the stress tensor components, summation is carried out on repeating indices and body-force distribution is zero. The boundary conditions used with system 14 are the following:

$$\left(\frac{\partial u_i}{\partial x_3}+ \frac{\partial u_3}{\par... ...\frac{2 \nu}{1-2\nu}\frac{\partial u_k}{\partial x_k}\delta_{i3}\vert _{z=z_0}= 0,$$

$$u_i(x,y,z_{\textrm{R}})= s_i(x,y),$$ (15)

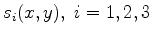where $s_i(x,y),\;i=1,2,3$ is a known displacement field at a fixed depth. Although system 14 is comprized of purely elastostatic equations, it allows us to model fluid-to-solid coupling via the boundary condition at 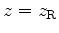$z=z_{\textrm{R}}$ that can be approximately computed using operator 5. For a laterally-homogeneous medium - or under the assumption of slow lateral variability and pseudo-differential operator ordering, (Maslov, 1976) - equations 14 can be Fourier-transformed in 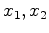$x_1,x_2$ , and the resulting system discretized in depth:

$$\frac{v_1(z+\Delta z)-v_1(z-\Delta z)}{2\Delta z}= v_4(z)$$

$$\frac{v_2(z+\Delta z)-v_2(z-\Delta z)}{2\Delta z}= v_5(z)$$

$$\frac{v_3(z+\Delta z)-v_3(z-\Delta z)}{2\Delta z}= v_6(z)$$

$$\frac{\mu(z+\Delta z)v_4(z+\Delta z)-\mu(z-\Delta z) v_4(z-\Delta z)}{2\Delta z}=$$

$$-(k_x^2+k_y^2+\frac{k_x^2}{1-2\nu(z)})\mu(z)v_1(z)-\frac{k_x k_y}{1-2\nu(z)}\mu(z)v_2(z)+\frac{i k_x}{1-2\nu}\mu(z)v_6(z)$$

$$\frac{\mu(z+\Delta z)v_5(z+\Delta z)-\mu(z-\Delta z)v_5(z-\Delta z)}{2\Delta z}=$$

$$-(k_x^2+k_y^2+\frac{k_y^2}{1-2\nu(z)})v_2(z)-\frac{k_x k_y}{1-2\nu(z)}v_1(z)+\frac{i k_y}{1-2\nu}v_6(z)$$

$$\frac{\mu(z+\Delta z)v_6(z+\Delta z)-\mu(z-\Delta z)v_6(z-\Delta z)}{2\Delta z}=$$

$$\frac{1}{1+\frac{1}{1-2\nu(z)}}\left[ -(k_x^2+k_y^2)v_3(z)+\frac{i k_x}{1-2 \nu(z)}v_4(z)+ \frac{i k_y}{1-2 \nu(z)}v_5(z)\right],$$ (16)

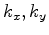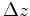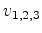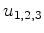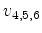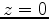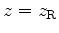where $k_x,k_y$ are the horizontal wavenumbers and $\Delta z$ is a depth step, $v_{1,2,3}$ are Fourier-transforms of the three displacement components $u_{1,2,3}$ and $v_{4,5,6}$ are their z-derivatives. At the boundaries $z=0$ and $z=z_{\textrm{R}}$ the central differences should be replaced with backward and forward differences (Iserles, 2008), and the boundary conditions 15 Fourier-transformed in a similar manner. In combination with the Fourier-transformed boundary conditions the above system is reduced to independent 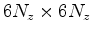$6N_z\times 6N_z$ linear systems for finding 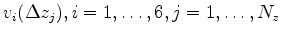$v_i(\Delta z_j),i=1,\ldots,6,j=1,\ldots,N_z$ for each wavenumber pair 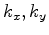$k_x,k_y$ , where 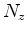$N_z$ is the number of depth steps.

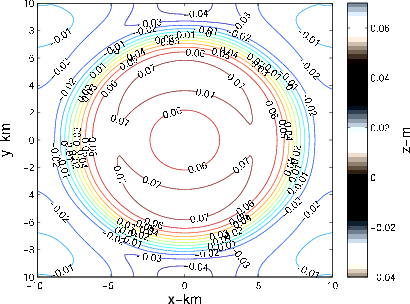
csubszdispoutsymhires Figure 11. Contour plot of the displacements modelled from the axisymmetric pore pressure decline of Fig 2(a).

csubszdispoutasymhires Figure 12. Contour plot of the displacements modelled from the asymmetric pore pressure decline of Fig 3(a).

Solution of the above system is efficiently parallelized, with individual 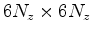$6N_z\times 6N_z$ sparse systems solved independently. Furthermore, each of the systems is banded with the bandwidth of 13 elements and therefore can be solved in a linear time and memory 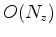$O(N_z)$ (Trefethen and Bau, 1997).

Fig 11 and Fig 12 show the results of modeling surface subsidence from the axisymmetric and asymmetric pore pressure decline synthetics of Fig 2(a) and Fig 3(a). Here 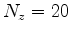$N_z=20$ with a 100 m depth step, the displacement field at the depth of 2 km was computed using operator 5. Although the above approach allows both elastic medium parameters (e.g., shear modulus 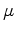$\mu$ and Poisson's ratio 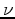$\nu$ ) to be vertically heterogeneous, the latter, as the ratio of the axial and transverse strains, is usually less affected by compaction, and hence we left it constant at 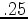$.25$ . However, the depth-dependent shear modulus is given by the formula

$$\mu(z)=\frac{23\texttt{GPa}}{1.+(z_{\textrm{R}}-z)/z_{\textrm{R}}}.$$ (17)

Comparison of Fig 11 and Fig 12 with the results of Fig 2(b) and Fig 3(b) obtained above using a homogeneous model indicate larger subsidence in the heterogenous case that is consistent with a greater compliance of the overburden as determined by the heterogeneous shear modulus of equation 17.

Although depth-varying models are common in geomechanical applications, and the diffusive nature of production-induced deformation favors slowly-varying models, there exist practical applications where strong lateral heterogeneity should be taken into account (for example, in subsalt regions). The widely accepted approach to tackling such problems consists of application of the finite elements method (Iserles, 2008) to the coupled poroelastic system (Kosloff et al., 1980). While finite elements can handle arbitrary spatial heterogeneity, the main disadvantage of this approach is the necessity to solve a potentially very large system of linear equations with very sparse but generally unstructured matrix.

A possible extension of our approach for tackling arbitrary heterogeneity could be summarized as follows. If system 14 can be factorized

$${\nabla} \cdot \mu(x_1,x_2,x_3)\left[\left(\frac{\partial u_i}{\p... ...ght)+\frac{2 \nu}{1-2\nu}\frac{\partial u_k}{\partial x_k}\delta_{ij} \right] =$$

$$\left( c_1\frac{\partial}{\partial x_3}+P_1(\frac{\partial}{\partial x_1},\frac{\partial}{\partial x_2})\right) \times$$

$$\left( c_2\frac{\partial}{\partial x_3}+P_2(\frac{\partial}{\partial x_1},\frac{\partial}{\partial x_2})\right) u,$$ (18)

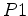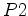where $P1$ and $P2$ are some pseudo-differential operators and 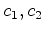$c_1,c_2$ are some functions, then given the boundary conditions 15, the boundary-value problem 14,15 can be solved by solving

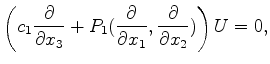$$\left( c_1 \frac{\partial}{\partial x_3}+P_1(\frac{\partial}{\partial x_1},\frac{\partial}{\partial x_2})\right)U=0,$$ (19)

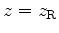upward, starting from the initial condition at depth $z=z_{\textrm{R}}$ , followed by solving

$$\left( c_2 \frac{\partial}{\partial x_3}+P_2(\frac{\partial}{\partial x_1},\frac{\partial}{\partial x_2})\right) u = U,$$ (20)

downward, starting from the free-surface boundary condition on the surface. Some factorisations 18 are trivial, as when the operator 20 maps the displacement field to the stress field, we effectively recover our original elastostatic system and obtain the well-known depth-extrapolation method for 6 variables (Segall, 2010). However, finding a factorisation that requires less than 6 variables may potentially lead to a method where the eigenmodes that correspond to exponentially increasing and decreasing solutions decouple in up and down-going extrapolation operators similar to the one-way wave equation (Claerbout, 2011). However, the author's attempts to construct linear operator factorisations 18 involving operators mapping only 3-component vector functions so far resulted in rank-deficient systems. The three displacement components may have to be complemented with an additional variable in order to achieve a pseudo-differential operator factorisation. The benefits of finding such factorisations and stable methods of solving factorized equations would extend beyond the solution of the uncoupled poroelastostatic system.

Identifying reservoir depletion patterns from production-induced deformations with applications to seismic imaging