|
|
|
|
Identifying reservoir depletion patterns from production-induced deformations with applications to seismic imaging |
We can use operator 4 for forward-modeling the displacement field from a specified pressure change. Note that operator 4 is a non-stationary convolutional integral operator for a homogeneous medium. The convolution is non-stationary due to the presence of 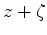 in the elastostatic Green's tensor. Integration along the horizontal axes can be accelerated by applying the operator in the wavenumber domain. However, integration along the vertical axis should still be carried out separately for different values of
in the elastostatic Green's tensor. Integration along the horizontal axes can be accelerated by applying the operator in the wavenumber domain. However, integration along the vertical axis should still be carried out separately for different values of 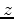 , hence the integration kernel is effectively four-dimensional. Assuming the reservoir to be thin in comparison with its lateral extents, which is always the case, we can replace the vertical integral with a mean value of the integrand times the reservoir thickness:
, hence the integration kernel is effectively four-dimensional. Assuming the reservoir to be thin in comparison with its lateral extents, which is always the case, we can replace the vertical integral with a mean value of the integrand times the reservoir thickness:
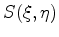 is the middle surface of the reservoir and
is the middle surface of the reservoir and
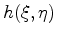 is the reservoir depth. For a non-flat reservoir,
is the reservoir depth. For a non-flat reservoir, 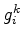 effectively depends not only on differences
effectively depends not only on differences 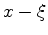 and
and 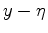 but on integration variables as well. In our implementation we compute 5 as a full convolutional operator, allowing slowly-varying asymptotics of the solutions by introducing scaling factors that depend on both
but on integration variables as well. In our implementation we compute 5 as a full convolutional operator, allowing slowly-varying asymptotics of the solutions by introducing scaling factors that depend on both 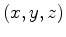 and
and
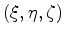 .
.
An implementation of this method is provided by the poroelastic_green.F90 module of the author's exp_tk Fortran 2003 object-oriented framework described in Appendix B.
We test our approach on synthetic data generated for a reservoir model based on the assumed geometry of the gas reservoir near Lacq, France, described by Segall et al. (1994). The reservoir is assumed to be anticlinal dome-shaped, with the depth of the reservoir approximated as
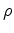 is the distance to the center of the reservoir, and all the distances are measured in km (see Fig 1). The reservoir thickness is estimated to be
is the distance to the center of the reservoir, and all the distances are measured in km (see Fig 1). The reservoir thickness is estimated to be
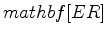 km. In the first test we apply the forward-modeling operator 5 to an axisymmetric synthetic pore pressure drop similar to the pore pressure change used by Segall et al. (1994) and given by
km. In the first test we apply the forward-modeling operator 5 to an axisymmetric synthetic pore pressure drop similar to the pore pressure change used by Segall et al. (1994) and given by
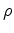 is the distance to the center of the reservoir. The result of displacement modeling using an
is the distance to the center of the reservoir. The result of displacement modeling using an
 reservoir grid and
reservoir grid and
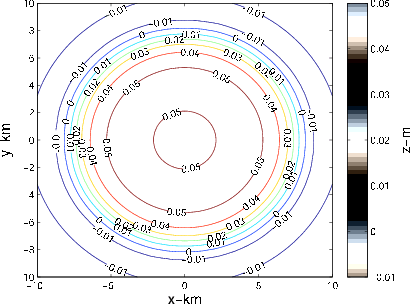
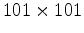 surface grid is shown on Fig 2(b). Linear poroelasticity predicts a linear relationship between the maximum subsidence and the maximum pore pressure decline. Segall et al. (1994) predicts that the subsidence rate for the axisymmetric model is bracketed between
surface grid is shown on Fig 2(b). Linear poroelasticity predicts a linear relationship between the maximum subsidence and the maximum pore pressure decline. Segall et al. (1994) predicts that the subsidence rate for the axisymmetric model is bracketed between 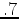 mm/MPa for the reservoir thickness of
mm/MPa for the reservoir thickness of 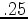 km and
km and 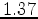 mm/MPa for the thickness of
mm/MPa for the thickness of 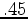 km. The subsidence rate indicated by Fig 2(b) for the value of the reservoir thickness of
km. The subsidence rate indicated by Fig 2(b) for the value of the reservoir thickness of 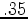 km is in a good agreement with that prediction.
i
km is in a good agreement with that prediction.
i
|
|---|
|
cppsymhires,csubsdispoutsymhires
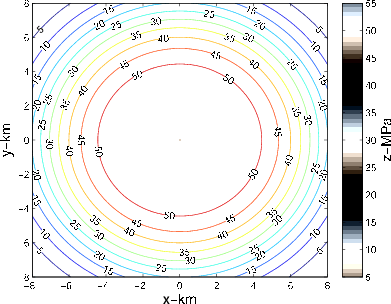
Figure 2. a) Contour plot of the axisymmetric pore pressure drop given by equation 7. b) Contour plot of the subsidence above the reservoir of Fig 1 due to the axisymmetric pore pressure decline of Fig 2(a). |
|
|
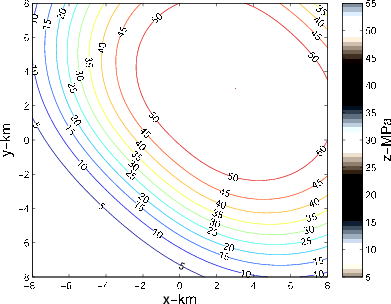
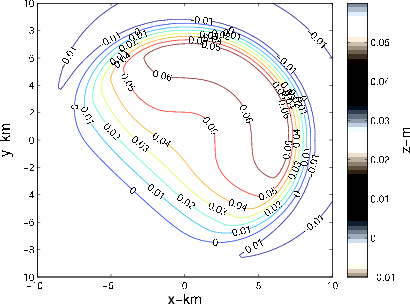
Next, we apply the modeling operator to the asymmetric synthetic pore pressure drop given by
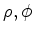 are the distance and azimuth from an off-centre point (3 km,3 km), with a steeper decline in pore pressure along the northeast-southwest directions (see Fig 3(a)). The pressure decline given by equation 8 is not based on any specific real-world example but is rather chosen as a somewhat extreme case of an asymmetric pressure decline pattern mismatching the reservoir geometry. The result of modeling displacements due to the asymmetric pore pressure decline within the reservoir, using the same reservoir and surface grids as above, is shown on Fig 3(b).
are the distance and azimuth from an off-centre point (3 km,3 km), with a steeper decline in pore pressure along the northeast-southwest directions (see Fig 3(a)). The pressure decline given by equation 8 is not based on any specific real-world example but is rather chosen as a somewhat extreme case of an asymmetric pressure decline pattern mismatching the reservoir geometry. The result of modeling displacements due to the asymmetric pore pressure decline within the reservoir, using the same reservoir and surface grids as above, is shown on Fig 3(b).
|
|---|
|
cppasymhires,csubsdispoutasymhires
Figure 3. a) Contour plot of the asymmetric pore pressure drop given by equation 8. b) Contour plot of the subsidence above the reservoir of Fig 1 due to the asymmetric pore pressure decline of Fig 3(a). |
|
|
The following table summarizes the medium parameters taken from (Segall et al., 1994) that are used in our tests:
| Parameter | SI | Imperial |
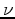
|
.25 | dimensionless |
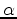
|
.25 | dimensionless |
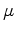
|
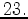 GPa
GPa |
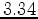 Mpsi
Mpsi |
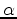 is computed as
is computed as
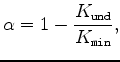 |
(9) |
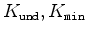 being the undrained bulk modulus and the bulk modulus of rock mineral grains, respectively (Mavko et al., 2009).
being the undrained bulk modulus and the bulk modulus of rock mineral grains, respectively (Mavko et al., 2009).
Modeling subsidence using operator 5, we are able to fully account for the asymmetric nature of the depletion pattern by using the most general form of Green's tensor for a homogeneous half-space. In that respect, our approach represents an advancement of the purely analytical techniques for axisymmetric reservoirs presented in (Geertsma, 1973) and (Segall et al., 1994). However, the assumption of homogeneity, which is required for our being able to use analytical expressions for the Green's tensor, is a serious limitation that may significantly impair the applicability of our method, especially bearing in mind that our ultimate objective is to estimate subsurface displacements from observable subsidence. Later in the paper we propose a computationally efficient extension of our method that is capable of tackling heterogeneity.
|
|
|
|
Identifying reservoir depletion patterns from production-induced deformations with applications to seismic imaging |