|
|
|
|
Image gather reconstruction using StOMP |
Donoho (2006) offers an approach termed compressive
sensing potential solution to this computation and storage problem.
In compressive sensing, a random subset of the desired measurements is made. An inversion problem
is then set up to estimate in an 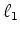 , or preferably
, or preferably 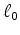 , sense, a sparse basis function that
fully characterizes the desired signal. For compressive sensing to work, a signal must be highly
compressible. For compressive
sensing to be worthwhile, the cost of inverting for the basis
function must be significantly less than the cost of acquiring the full signal.
Clapp (2011) showed that correlation gather construction fit
the first criteria for a successful compressive sensing problem. Multi-dimensional
correlation gathers/angle gathers are compressible at nearly a 100:1 ratio. The
challenge became finding an inversion scheme that could accurately enough recover
the full model. Donoho et al. (2006) proposed a solution to the second problem,
an
, sense, a sparse basis function that
fully characterizes the desired signal. For compressive sensing to work, a signal must be highly
compressible. For compressive
sensing to be worthwhile, the cost of inverting for the basis
function must be significantly less than the cost of acquiring the full signal.
Clapp (2011) showed that correlation gather construction fit
the first criteria for a successful compressive sensing problem. Multi-dimensional
correlation gathers/angle gathers are compressible at nearly a 100:1 ratio. The
challenge became finding an inversion scheme that could accurately enough recover
the full model. Donoho et al. (2006) proposed a solution to the second problem,
an 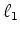 version methodology that works for a large number of unknowns.
In this paper, I apply the Stagewise Orthogonal Matching Pursuit (StOMP)
algorithm to correlation gather reconstruction.
I show that the angle domain representation of the sparsely acquired
gathers is similar to the representation of the full data. I then apply
a phase encoding technique, combining many different correlations to every
data point to further improve the inverted model.
version methodology that works for a large number of unknowns.
In this paper, I apply the Stagewise Orthogonal Matching Pursuit (StOMP)
algorithm to correlation gather reconstruction.
I show that the angle domain representation of the sparsely acquired
gathers is similar to the representation of the full data. I then apply
a phase encoding technique, combining many different correlations to every
data point to further improve the inverted model.
|
|
|
|
Image gather reconstruction using StOMP |