 |
 |
 |
 | Angle-domain illumination gathers by wave-equation-based methods |  |
![[pdf]](icons/pdf.png) |
Next: Angle-domain image and illumination
Up: Tang and Biondi: Angle-dependent
Previous: introduction
Linearized modeling (Born modeling) from a prestack image parameterized as a function of subsurface offset can
be described as follows:
 |
|
|
(1) |
where
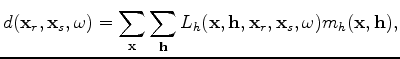 is the seismic data with a source located at
is the seismic data with a source located at
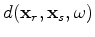 and a receiver
located at
and a receiver
located at
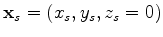 ;
; 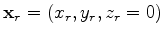 is the angular frequency;
is the angular frequency;
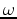 is the prestack image located at
is the prestack image located at
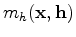 for a half subsurface offset
for a half subsurface offset
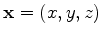 ;
;
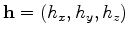 is the sensitivity kernel defined as follows:
is the sensitivity kernel defined as follows:
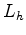 |
|
|
(2) |
where
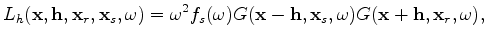 is the source signature, and
is the source signature, and
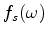 and
and
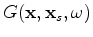 are the Green's functions connecting the source and receiver, respectively,
to the image point
are the Green's functions connecting the source and receiver, respectively,
to the image point 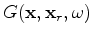 .
.
Reconstruction of the prestack image
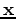 can be posed as an inverse problem by minimizing the following objective function
defined in the data space:
can be posed as an inverse problem by minimizing the following objective function
defined in the data space:
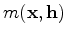 |
|
|
(3) |
where
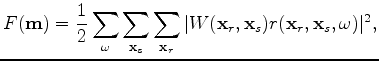 is the data residual
and
is the data residual
and
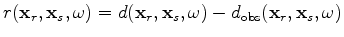 is the acquisition mask operator, which contains unity values where we record data and zeros where
we do not.
The gradient of the objective function
is the acquisition mask operator, which contains unity values where we record data and zeros where
we do not.
The gradient of the objective function 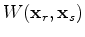 reads
reads
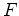 |
|
|
(4) |
where 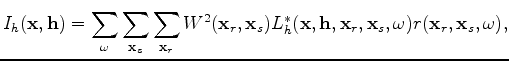 denotes complex conjugation.
Equation 4 is similar to the prestack shot-profile migration formula and it produces migrated reflectivity images
defined in the subsurface offset domain (Rickett and Sava, 2002).
denotes complex conjugation.
Equation 4 is similar to the prestack shot-profile migration formula and it produces migrated reflectivity images
defined in the subsurface offset domain (Rickett and Sava, 2002).
The Hessian can be obtained by taking the second-order derivatives of 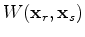 with respect to the model parameters as follows:
with respect to the model parameters as follows:
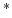 |
|
|
(5) |
When
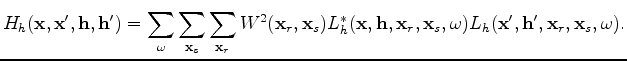 and
and
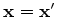 , we obtain the diagonal elements of the Hessian operator
, we obtain the diagonal elements of the Hessian operator
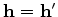 |
|
|
(6) |
The diagonal of the Hessian is often known as the illumination map of the subsurface,
it contains illumination contribution from both sources and receivers for a given acquisition configuration.
 |
 |
 |
 | Angle-domain illumination gathers by wave-equation-based methods |  |
![[pdf]](icons/pdf.png) |
Next: Angle-domain image and illumination
Up: Tang and Biondi: Angle-dependent
Previous: introduction
2010-05-19
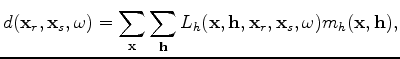 is the seismic data with a source located at
is the seismic data with a source located at
![]() can be posed as an inverse problem by minimizing the following objective function
defined in the data space:
can be posed as an inverse problem by minimizing the following objective function
defined in the data space:
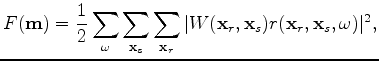 is the data residual
and
is the data residual
and
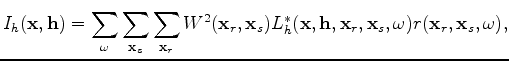 denotes complex conjugation.
Equation 4 is similar to the prestack shot-profile migration formula and it produces migrated reflectivity images
defined in the subsurface offset domain (Rickett and Sava, 2002).
denotes complex conjugation.
Equation 4 is similar to the prestack shot-profile migration formula and it produces migrated reflectivity images
defined in the subsurface offset domain (Rickett and Sava, 2002).
![]() with respect to the model parameters as follows:
with respect to the model parameters as follows:
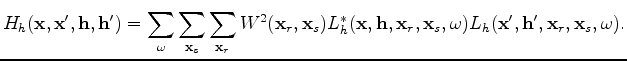 and
and