Implicit finite difference in time-space domain with the helix transform

Non-separability of velocity from factorized implicit coefficients

The initial impetus for using deconvolutions by spectrally factorized coefficients of an implicit finite-difference scheme to approximate the 2-way wave equation was that the velocity could be separated from the scheme's coefficients. The hope was that if this was possible, a filter with constant coefficients could be created to handle propagation through a variable velocity medium. This has turned out to not be the case, at least for the formulation of the implicit scheme in Equation 9. If we look at the left hand side of Equation 17:

$$\left( \begin{array}{cccccc} 1+4\alpha & -\alpha & \dots & -\alph... ...t+1}_1 P^{t+1}_2 P^{t+1}_3 P^{t+1}_4 P^{t+1}_5 \end{array} \right).$$ (18)

It is clearly impossible to divide the system by 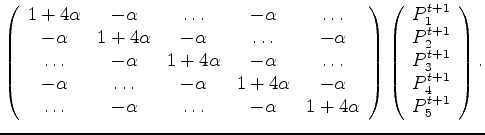$\alpha$ or any of it's constituent parts (in particular - the velocity) without changing the value of the diagonal weight. If the velocity is variable, this will result in a different set of finite-difference weights at various lines of the linear system in (17), requiring a different set of spectrally factorized coefficients wherever the velocity changes.

The option of using a ``filter bank'' for different parts of the wavefield according to the local velocity has already been discussed in Rickett et al. (1998), for wave propagation in the frequency-wavenumber domain. This may also be applicable to propagation in the time-space domain, but I have not yet tested it. It was my hope that this would be unecessary, and that a single set of filter coefficients could be utilized for the entire wavefield irrespective of velocity. This would make the propagation algorithm simpler, and more amenable to future parallelization schemes.

Implicit finite difference in time-space domain with the helix transform