Joint least-squares inversion of up- and down-going signal for ocean bottom data sets

Introduction

Ocean-bottom seismic (OBS) acquisition is an established technology in which seismometers are placed at the sea bottom and shots are fired at the sea surface. In areas congested by platforms or other obstacles, ocean bottom seismic is advantageous because it is operated by small boats without cumbersome towed streamers. Such a geometry enables OBS acquisition to provide wide-azimuth illumination, shear-wave recording, a quieter recording environment, higher-resolution data and improved repeatability. Therefore, it is used for imaging in obstructed oilfields and for time-lapse monitoring of hydrocarbon reservoirs.

There are different processing schemes for ocean bottom data. The traditional way, inherited from surface seismic processing, is to remove all free-surface multiples and to migrate only with the primary signal (Wang et al., 2009). Therefore, initial work on OBS data processing has been dedicated to the removal of free-surface multiples. One way to attenuate strong free-surface multiples is to combine the geophone and hydrophone recordings to eliminate the receiver ghost and the water column reverberations, a technique known as PZ summation (Barr and Sander, 1989; Schalkwijk et al., 1999; Soubaras, 1996). Such a technique uses the polarity difference between a scalar measurement (pressure) and a vector measurement (velocity). As an alternative to PZ summation, Sonneland and Berg (1987) and Amundsen (2001) address free-surface multiples with the theory of up-down deconvolution in both layered and complex media. In this approach, not only are all free-surface multiples attenuated, but also de-ghosting and signature deconvolution are conducted in a single step.

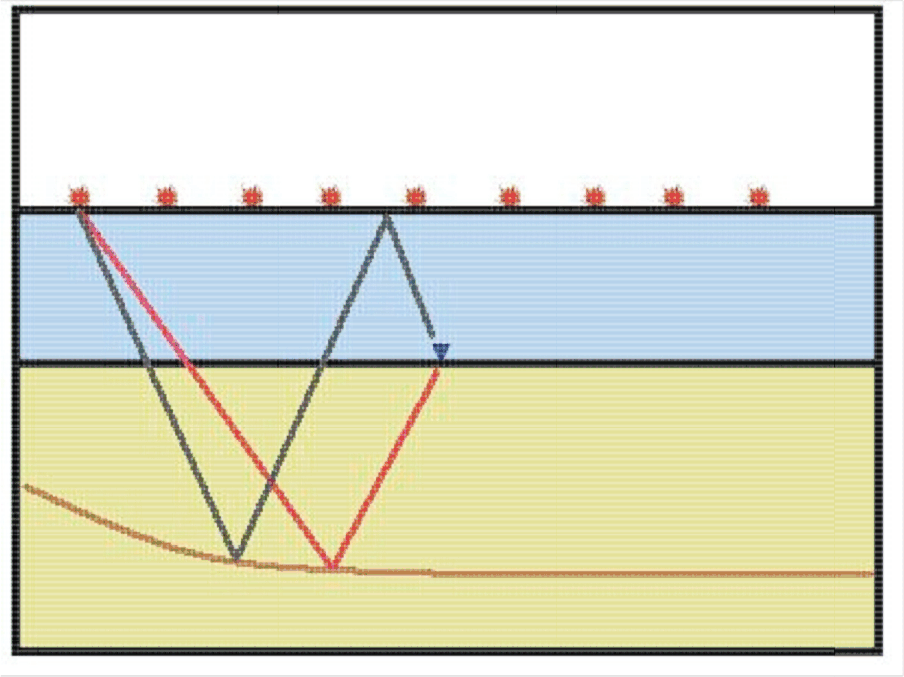
While multiples are often treated as noise, they are formed by the same source signal as primaries but travel along different paths in the medium. The receiver ghost, also known as the mirror signal, is the next order of reflection beyond the primaries with an additional reflection off the sea surface. In a deep water OBS survey, the source grid has a much wider lateral extend than the receiver grid. Therefore, the subsurface reflection point of the receiver ghost is located at greater distances from the receiver station than the primaries Figure 1. Therefore, the mirror signal can provide a wider subsurface illumination than the primaries if the energy is properly migrated. Several authors have used the mirror signal in the migration of OBS data (Grion et al., 2007; Dash et al., 2009; Ronen et al., 2005; Godfrey et al., 1998).

illum
Figure 1. The subsurface reflection point of the receiver ghost, also known as the mirror signal (in black), is located at a greater distance from the receiver station than the primary signal (in red). For a deep water OBS survey, the source grid has a much wider lateral extend than the receiver grid. This translates to a wider subsurface illumination for the mirror signal than the primaries.

While most authors conclude that the mirror image gives a better result than the conventional primary image, the information in the primary image is also valuable. The primary ray path is shorter than the mirror ray path, which contributes to a higher signal-to-noise ratio in the primary signal. In a common receiver gather, the illumination points of the subsurface by each source-receiver pair are closer together in the primary reflection than in the mirror reflection. This translates to higher image quality in the region illuminated by the primary. Instead of treating the primary image and the mirror image separately, we propose an iterative linear least-squares inversion scheme that combines the primary and the mirror image. Such an inversion can improve the structure and aperture of the seismic images by using two sets of signals: the up-going primaries and the down-going mirror signals.

Muijs et al. (2007) made an early attempt to image primary and free-surface multiples together. It requires the data to be decomposed into up-going and down-going constituents, followed by downward extrapolation and a 2D deconvolution based imaging condition. While this technique is computationally efficient, its image contains crosstalk artifacts caused by interference of up-going and down-going waves not associated with the same subsurface reflector. In contrast to Muijs' method, joint inversion can optimally combine structural information provided by two types of reflection that are free from crosstalk.

In this paper, we focus on the joint inversion of the acoustic (P) wave signal. We first discuss the theory of the joint linear least-squares inversion. We then apply the inversion scheme to two modified versions of the 2D Marmousi model and show the overall improvement of the joint inversion result.

Joint least-squares inversion of up- and down-going signal for ocean bottom data sets