|
|
|
|
Geophysical applications of a novel and robust L1 solver |
Velocity analysis is one the most critical and problematic procedures in seismic exploration. In data with noise bursts, velocity analysis is prone to error and even unrealistic results. Therefore, to handle this problem robustly, we formulate velocity analysis as an inversion problem as follows:
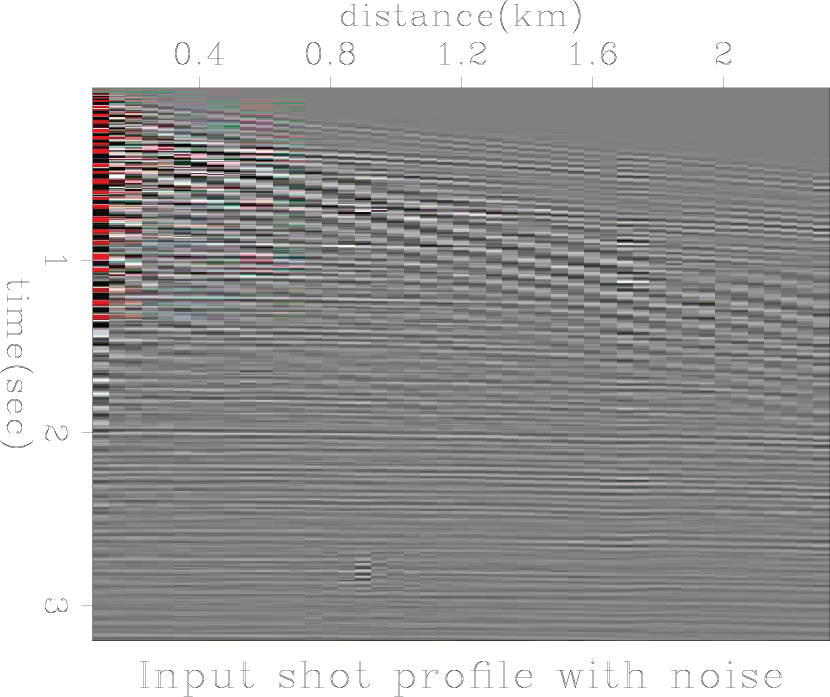
Figure 6 shows a shot gather from Yilmaz's dataset. There are two distinct types of noise in these data: first is the linear noise caused by all kinds of surface waves, which can be attenuated by taking advantage of their physical properties; second is the abnormally high-amplitude burst noise at the near offsets, which is difficult to fit into a statistical model.
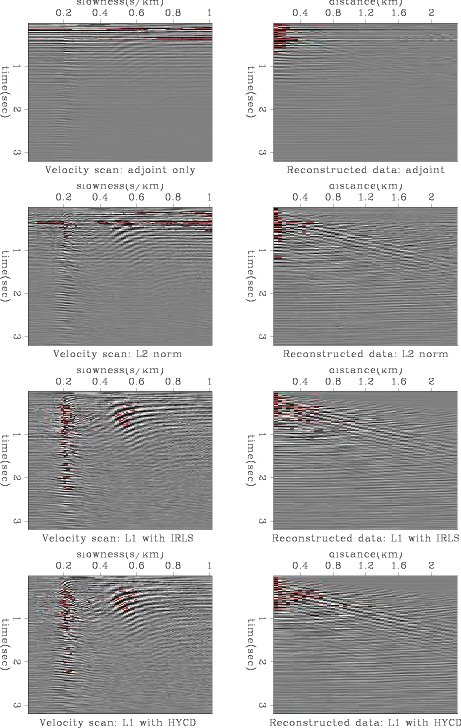
Figure 7 shows the inversion results for different methods. Because of the existence of the high amplitude noise at the near-offset, a velocity scan without inversion yields no meaningful result. For the L2 inversion, the noise has contaminated the whole panel, making it impossible to see the velocity trend. The inversion results of both IRLS and HYCD show clear velocity trends, and the near-offset burst noise is successfully removed in the reconstructed data.
|
|---|
|
noizin
Figure 6. Input shot profile with noise.The red points in the figure indicates the data points with very high amplitude. |
|
|
|
|---|
|
real
Figure 7. Inversion results of different methods. The red points in the figure indicates the data points with very high amplitude. Panels in the left column are the results of velocity scans, while panels on the right are the corresponding reconstructed data. First row: No inversion is applied (adjoint only); Second row: Inversion results by CD with L2; Third row: Inversion results by hybrid with IRLS; Bottom row: Inversion results by CD with L1. |
|
|
|
|
|
|
Geophysical applications of a novel and robust L1 solver |