Blocky velocity inversion by hybrid norm

Introduction

Most inversion problems try to correct for the fact that the adjoint is different than the inverse. However, in the case of the Dix formula (Dix, 1952), an exact inverse exists. The problem with the Dix formula is that it requires noise-free RMS velocity as an input. Real data always contains some level of noise. In addition, stacking velocity is measured from the data and used as the RMS velocity, even though these values can differ significantly. Therefore, the Dix formula is usually cast as an inverse problem. The conventional regularized Dix inversion (Harlan, 1999; Clapp, 2001; Koren and Ravve, 2006) produces smooth results because the inversion is optimized using the 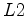$L2$ norm. However, there are many situations, such as salt boundaries and faults, in which sharp boundaries (i.e. blocky models) are more geologically realistic.

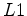Previous work has shown that the $L1$ norm can produce sparse and blocky results. However, $L1$ norm solvers can encounter stability and convergence issues, since the objective function defined by that norm is at the verge of convexity. Claerbout (2009) has proposed a hybrid $L1/L2$ norm in which a smooth transition between $L1$ and $L2$ can be set at any desired percentile; the hybrid norm has better convergence and stability properties than a pure $L1$ norm. Also, Maysami and Moussa (2009) describe a conjugate-direction solver in which the hybrid $L1/L2$ norm is optimized using Taylor's expansion.

Previously, Li and Maysami (2009) showed that blockiness can be achieved in 1D using a first derivative operator to regularize the problem. In this paper, we expand blockiness to 2D by testing different regularizations on two field datasets.

Blocky velocity inversion by hybrid norm