 |
 |
 |
 | Selecting the right hardware for Reverse Time Migration |  |
![[pdf]](icons/pdf.png) |
Next: Bottlenecks
Up: Clapp et al.: Hardware
Previous: Introduction
The concept behind RTM is relatively simple.
We start with a known earth model. This earth model might be simply
acoustic velocity but can be anisotropic, elastic, or even visco-elastic.
Two different modeling experiments are conducted
simultaneously through the earth model. Both attempt to simulate the
seismic experiment conducted in the field, one from
the perspective of the source and one from the perspective
of the receivers.
The source experiment involves injecting our estimated source
wavelet into the earth and propagating it from 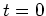 to our maximum
recording time
to our maximum
recording time 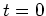 , creating a 4-D source field
, creating a 4-D source field
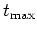 . At the same time, we conduct the receiver experiment.
We inject and propagate our recorded data starting from
. At the same time, we conduct the receiver experiment.
We inject and propagate our recorded data starting from 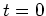 to
to 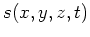 ,
creating a similar four dimensional volume
,
creating a similar four dimensional volume 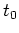 .
The most common approach is to propagate these fields using an
explicit time marching scheme (Dablain, 1986).
We start from the acoustic wave equation
.
The most common approach is to propagate these fields using an
explicit time marching scheme (Dablain, 1986).
We start from the acoustic wave equation
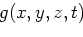 |
(1) |
where 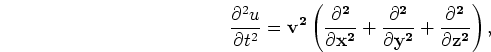 is pressure and
is pressure and 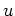 is velocity. We can
use a Taylor expansion to approximate these derivatives.
Algorithm 2
shows the pseudo-code for
how to forward propagate by
is velocity. We can
use a Taylor expansion to approximate these derivatives.
Algorithm 2
shows the pseudo-code for
how to forward propagate by 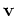 steps a source
function
steps a source
function 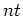 , with a
, with a 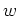 interval
on a regular mesh whose
size is
interval
on a regular mesh whose
size is 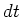 indexed by
indexed by 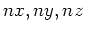 ,
using a
second-order approximation of the
time and space derivatives.
,
using a
second-order approximation of the
time and space derivatives.
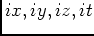
We have a reflection
where the energy propagated from the source and the receiver are located at
the same position
at the same time. The final image  is the summation of
correlating the source and receiver wavefield at every time and
every shot,
is the summation of
correlating the source and receiver wavefield at every time and
every shot,
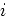 |
(2) |
Subsections
 |
 |
 |
 | Selecting the right hardware for Reverse Time Migration |  |
![[pdf]](icons/pdf.png) |
Next: Bottlenecks
Up: Clapp et al.: Hardware
Previous: Introduction
2009-10-16
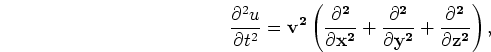 is pressure and
is pressure and  is the summation of
correlating the source and receiver wavefield at every time and
every shot,
is the summation of
correlating the source and receiver wavefield at every time and
every shot,