RMO analysis in ADCIGs

When the migration velocity is correct and the image is focused at zero subsurface offset, transformation to the angle domain does not change the image-point depth and the reflections are imaged at the same depth for all aperture angles ($z_{\widetilde{\gamma}}=z_\xi=const$). As a consequence, when migrated with the correct migration velocity, reflectors are mapped flat in ADCIGs. In contrast, when the reflections are not focused at zero offset, transformation to the angle domain maps the events to different depths for each different angle. The image-depth variability with aperture angle is described by the RMO function, which we want to measure and quantify as a function of the perturbation in anisotropic parameters. Below, we summarize the approach given by Biondi (2005a) to derive the expression of RMO in anisotropic ADCIGs. It consists of approximating the RMO by the first-order Taylor series expansion about the correct migration velocity.

The notation used in Biondi (2005a) is the following: the VTI velocity function parameterization is ${\bf V}=(V_V,V_H,V_N)$,where V_V is the velocity of a vertical ray, V_H is the velocity of a horizontal ray and V_N is the NMO velocity. It is equivalent to Thomsen's parameterization ${\bf V}=(V_V,\epsilon,\delta)$, since $V_H=V_V \sqrt{1+2\epsilon}$ and $V_N=V_V\sqrt{1+2\delta}$.

We define the perturbations in the VTI velocity function as a three-component vector = $\left(\rho_V_V,\rho_V_H,\rho_V_N\right)$, where each component is a multiplicative factor for each migration velocity. The vector generates a perturbed velocity field, $_\rho{\bf V}$ defined by $_\rho{\bf V}=\left({_\rho}V_V,{_\rho}V_H,{_\rho}V_N\right) =\left(\rho_V_VV_V,\rho_V_HV_H,\rho_V_NV_N\right)$.

From the analytic expression of the impulse response (derived from Figure ) and geometric interpretation of the angle-domain transformation, Biondi (2005a) derives the first-order derivatives of the image depth in the angle domain with respect to anisotropic parameter perturbations:

$$\begin{eqnarray} \frac{\partial z_{\widetilde{\gamma}}}{\partial \rho_{i}} = -z_... ...) } { S\left(\gamma\right) } \frac{\partial S}{\partial \rho_{i}},\end{eqnarray}$$ (5)

where S is the slowness along the source and receiver rays.

Similarly, because residual moveout $\Delta z_{\rm RMO}$ is defined as the difference between the reflector movement at finite angle ($\widetilde{\gamma}$) and the reflector movement at normal incidence ($\widetilde{\gamma}=0$), from equation 5, we can express the first-order derivatives of the residual moveout with respect to anisotropic parameter perturbations:

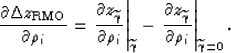$$\begin{eqnarray} \frac{\partial \Delta z_{\rm RMO}}{\partial \rho_{i}} = \left. ... ...{\gamma}}}{\partial \rho_{i}} \right\vert _{\widetilde{\gamma}=0}.\end{eqnarray}$$ (6)

The residual moveout $\Delta z_{\rm RMO}$ is eventually approximated by the first-order Taylor series expansion about the correct migration velocity (${\bf \rho}={\bf 1}$). The linearized expression is the following:  

$$\Delta z_{\rm RMO}=\left.\frac{\partial \Delta z_{\rm RMO}}{... ...\widetilde{\gamma},{\bf \rho}={\bf 1}} \left(\rho_V_N-1\right).$$ (7)