Now the trick to get from horizontal fractures and VTI to
aligned vertical fractures and HTI symmetry is relatively simple.
We will not need to make any effort to relabel the cij's.
Rather we just change the meaning of the labels. As long as we
stay mentally oriented in the reference frame of the fractures
themselves, we can continue to view the z-direction as the symmetry axis
and the xy-plane, as the plane of the fractures. The only change we
need to make arises from the fact that the surface, where we shoot our
seismic survey, is now at 90o from the fracture plane, whereas for
horizontal fractures the surface was at 0o from the fracture plane.
This observation implies that, wherever the angle
![]() (measured in radians) appeared in our previous formulas,
now we must replace it by
(measured in radians) appeared in our previous formulas,
now we must replace it by ![]() radians. Thus,
radians. Thus,
![]() and vice versa in the formulas.
This algorithm is exactly right only for those planes that are vertical
and also perpendicular to the fracture plane, i.e., at azimuthal angles
and vice versa in the formulas.
This algorithm is exactly right only for those planes that are vertical
and also perpendicular to the fracture plane, i.e., at azimuthal angles
![]() . For all angles, we actually need to replace
. For all angles, we actually need to replace
![]() by
by ![]() .Then, when
.Then, when ![]() or
or ![]() , there is no angular dependence
since we are in the plane of the fracture.
, there is no angular dependence
since we are in the plane of the fracture.
For the ![]() dependence, taking
dependence, taking ![]() ,is actually a handier way to proceed, because then we can reduce all the
formulas to the same equivalent form as the one Thomsen had originally
chosen -- if we choose to do so. It is also helpful to backup one step
in the Thomsen derivation and restore squares, thereby ``unexpanding''
the square root. Certain approximations are then undone, and the final
formulas we obtain will be more accurate.
,is actually a handier way to proceed, because then we can reduce all the
formulas to the same equivalent form as the one Thomsen had originally
chosen -- if we choose to do so. It is also helpful to backup one step
in the Thomsen derivation and restore squares, thereby ``unexpanding''
the square root. Certain approximations are then undone, and the final
formulas we obtain will be more accurate.
If ![]() ,
, ![]() , and
, and ![]() are the Thomsen parameters for
the VTI symmetry (horizontal fracture), then, for example,
are the Thomsen parameters for
the VTI symmetry (horizontal fracture), then, for example,
| |
(12) |
Similar calculations for vp2 and vsv2 give
| |
(13) |
| |
(14) |
Examples of these results for small (![]() ) and
higher (
) and
higher (![]() ) crack densities [see Berryman
and Grechka (2006) for details of the methods used to obtain
all the Sayers and Kachanov crack-influence parameters from
simulation data and Berryman (2007)
for a full discussion of the reservoir application] are presented in Figures 1-6.
) crack densities [see Berryman
and Grechka (2006) for details of the methods used to obtain
all the Sayers and Kachanov crack-influence parameters from
simulation data and Berryman (2007)
for a full discussion of the reservoir application] are presented in Figures 1-6.
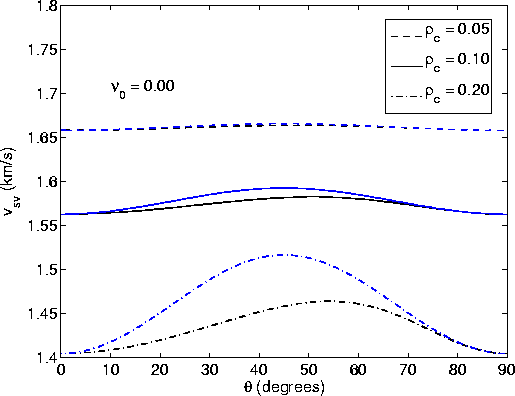 |
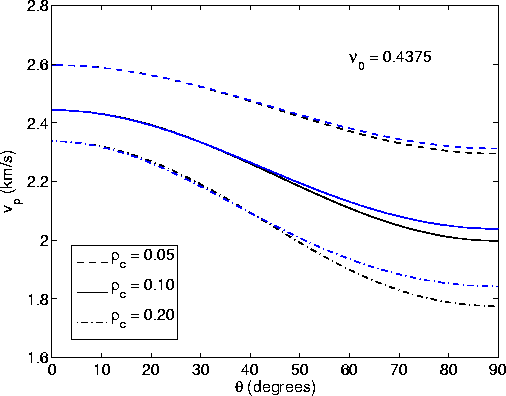 |