![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the AMO impulse responses obtained with
the filters in equation
compares the AMO impulse responses obtained with
the filters in equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (top) and equation
(top) and equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (bottom).
Both are obtained with a value of
(bottom).
Both are obtained with a value of
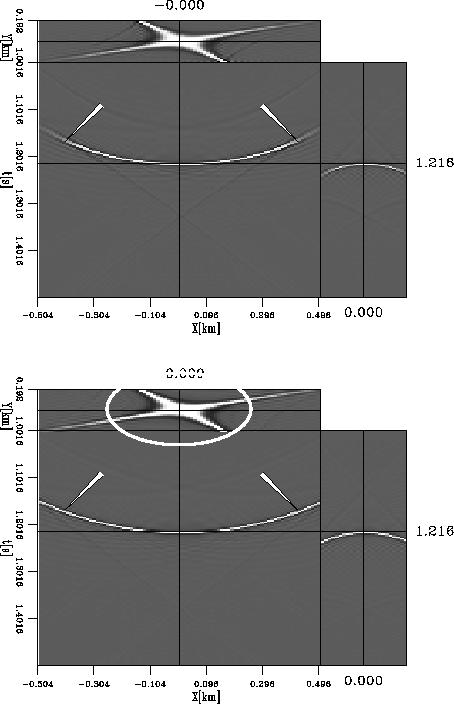
To better understand the PS-AMO operator, I compute and
analyze its impulse response.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the AMO impulse responses obtained with
the filters in equation
compares the AMO impulse responses obtained with
the filters in equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (top) and equation
(top) and equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (bottom).
Both are obtained with a value of
(bottom).
Both are obtained with a value of ![]() and vp=2.0 km/s, and are
kinematically equivalent.
and vp=2.0 km/s, and are
kinematically equivalent.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents a similar comparison to
Figure
presents a similar comparison to
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) for the case of converted waves. Here,
we use
for the case of converted waves. Here,
we use ![]() and vp=2.0 km/s. Both impulse responses,
Figures
and vp=2.0 km/s. Both impulse responses,
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , also
illustrate the differences in the dynamic
behavior of the operator. The top panels for both figures show
the impulse responses using the operator from equation
, also
illustrate the differences in the dynamic
behavior of the operator. The top panels for both figures show
the impulse responses using the operator from equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , which is
based on the known PS-DMO operator of Xu et al. (2001). In contrast,
the bottom panels show the PS-AMO operator
from equation
, which is
based on the known PS-DMO operator of Xu et al. (2001). In contrast,
the bottom panels show the PS-AMO operator
from equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , which is based on
the new PS-DMO operator, presented in Chapter 2, equivalent to the Zhou et al. (1996) PP-DMO operator.
The arrows in Figures
, which is based on
the new PS-DMO operator, presented in Chapter 2, equivalent to the Zhou et al. (1996) PP-DMO operator.
The arrows in Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show that
the operator from equation
show that
the operator from equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) has stronger amplitudes
for steeply dipping events than the operator from equation
has stronger amplitudes
for steeply dipping events than the operator from equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The area marked by the oval in the bottom panel for both
Figures
.
The area marked by the oval in the bottom panel for both
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows that impulse response for the PS-AMO operator
is not center at zero inline and crossline midpoint location, as
it is the case of the PP-AMO operator.
shows that impulse response for the PS-AMO operator
is not center at zero inline and crossline midpoint location, as
it is the case of the PP-AMO operator.
 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (top),
and filter in equation
(top),
and filter in equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (bottom), both with
(bottom), both with 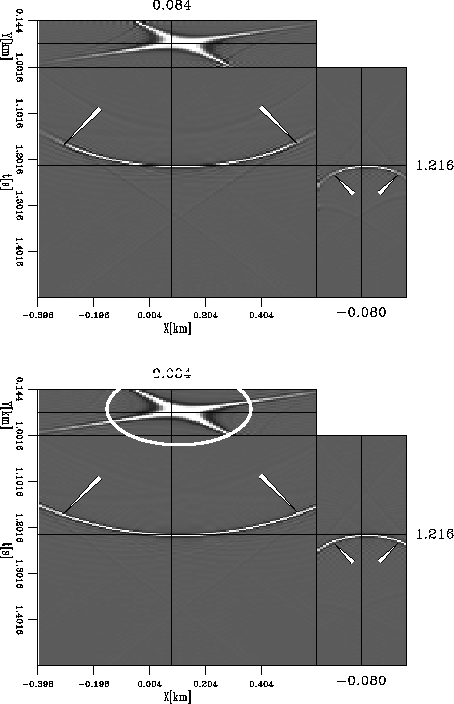 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (top),
and filter in equation
(top),
and filter in equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (bottom), with
(bottom), with ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) the new filter has more energy
at high dip values. It is also possible to note the asymmetric behavior of the
PS-AMO operator.
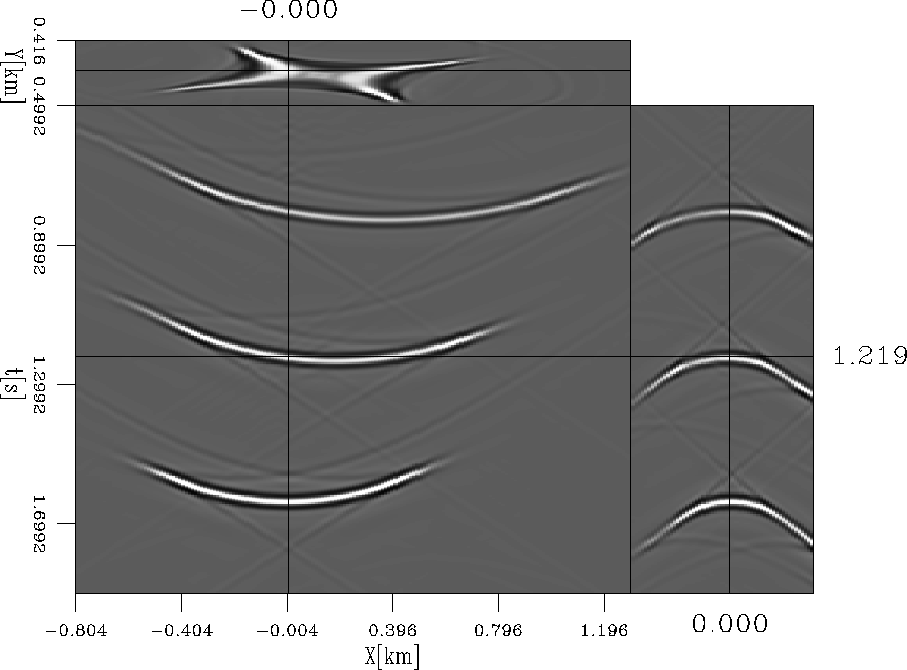
This is an unfold 3-D cube representation of the results. The crossing solid lines represent
position of the unfold planes.
the new filter has more energy
at high dip values. It is also possible to note the asymmetric behavior of the
PS-AMO operator.
This is an unfold 3-D cube representation of the results. The crossing solid lines represent
position of the unfold planes.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows two important characteristics of PS-AMO. First, the
PS-AMO operator is asymmetric because of the difference between the downgoing and upgoing
raypaths. Second, the PS-AMO operator varies with respect to traveltime, even for a constant velocity medium;
this behavior is caused by all the non-linear dependencies of the PS-AMO operator
with respect to traveltime, P velocity, and
shows two important characteristics of PS-AMO. First, the
PS-AMO operator is asymmetric because of the difference between the downgoing and upgoing
raypaths. Second, the PS-AMO operator varies with respect to traveltime, even for a constant velocity medium;
this behavior is caused by all the non-linear dependencies of the PS-AMO operator
with respect to traveltime, P velocity, and ![]() . The vertical variation of
the lateral shift reflects that the lateral displacement between
the CMP and CRP also varies with the traveltime. Both characteristics are
intrinsic of converted-wave data.
. The vertical variation of
the lateral shift reflects that the lateral displacement between
the CMP and CRP also varies with the traveltime. Both characteristics are
intrinsic of converted-wave data.
 |