




Next: synthetic data examples
Up: Tang: Regularized inversion
Previous: regularized least-squares inversion
Solving fitting goals (37) and (38) is expensive, since we have to propagate wavefields downward
and upward within each iteration, with the cost for each iteration equal to the cost of two migrations.
For small-scale problems, it is solvable;
for large-scale problems, however, the computational cost might be prohibitive. What's more, currently there are no
universal criteria for choosing the hyperparameters:
 , which balances the data-fitting goal and the model-styling goal, and
, which balances the data-fitting goal and the model-styling goal, and  , which controls
the sparseness of the model space. They can be decided only by trial and error, which obviously is not
practical for very large-scale problems.
, which controls
the sparseness of the model space. They can be decided only by trial and error, which obviously is not
practical for very large-scale problems.
Instead of propagating wavefields at each iteration, however, we can precompute the Hessian or approximate
it with a diagonal matrix
and then solve the modified fitting goals iteratively. The solution of fitting goal (37) in the
least-squares sense is
| 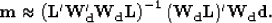 |
(40) |
The weighted Hessian matrix 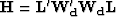 can be either fully computed Valenciano and Biondi (2004) or
approximated with a diagonal matrix; here I do the latter,
approximating the weighted Hessian with its diagonals as follows Rickett (2003):
can be either fully computed Valenciano and Biondi (2004) or
approximated with a diagonal matrix; here I do the latter,
approximating the weighted Hessian with its diagonals as follows Rickett (2003):
| 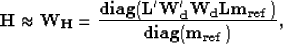 |
(41) |
and I choose the migrated image cube as the reference image cube:
| 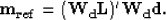 |
(42) |
Therefore, fitting goals (37) and (38) can be modified as follows:
| 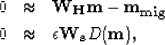 |
(43) |
| (44) |
where 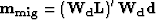 , which is obtained by migrating the recorded data.
To avoid the right-hand side of equation (41) being divided by zeros,
I multiply
, which is obtained by migrating the recorded data.
To avoid the right-hand side of equation (41) being divided by zeros,
I multiply 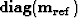 on both sides of equation (43),
resulting in
on both sides of equation (43),
resulting in
| 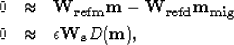 |
(45) |
| (46) |
where 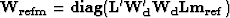 and
and 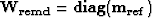 . Fitting goals
(45) and (46) can be solved by using the IRLS algorithm described in the previous section.
. Fitting goals
(45) and (46) can be solved by using the IRLS algorithm described in the previous section.





Next: synthetic data examples
Up: Tang: Regularized inversion
Previous: regularized least-squares inversion
Stanford Exploration Project
1/16/2007
![]() , which balances the data-fitting goal and the model-styling goal, and
, which balances the data-fitting goal and the model-styling goal, and ![]() , which controls
the sparseness of the model space. They can be decided only by trial and error, which obviously is not
practical for very large-scale problems.
, which controls
the sparseness of the model space. They can be decided only by trial and error, which obviously is not
practical for very large-scale problems.