




Next: APPENDIX C. DISCUSSION OF
Up: Berryman and Grechka: Random
Previous: Self-consistent Estimates for Hexagonal
Sayers and Kachanov (1991) present a useful method for
decomposing the elastic potential of a cracked system into parts due
to the (assumed) homogeneous and isotropic elastic background
material, and those due to the presence of cracks up to moderate densities.
The fundamental idea is that the elastic potential function is composed
of just nine terms, representing all combinations of stress invariants of
such a system. These invariants depend on the stress tensor  and the crack density tensor
and the crack density tensor  . In particular, the tensor
. In particular, the tensor
 is defined in three dimensions by
is defined in three dimensions by
| 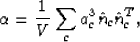 |
(37) |
where V is the averaging volume, 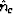 is the unit normal of
penny-shaped crack c having radius ac. We use the notation
is the unit normal of
penny-shaped crack c having radius ac. We use the notation
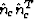 , where T is the transpose, to express the
outer product (
, where T is the transpose, to express the
outer product (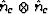 )of two vectors; this notation is consistent with that
commonly used to express the singular value decomposition of an
arbitrary matrix in terms of its singular vectors. Another common, and
entirely equivalent, form of notation for the same quantity that is
often used in the mechanics literature is the dyadic
form
)of two vectors; this notation is consistent with that
commonly used to express the singular value decomposition of an
arbitrary matrix in terms of its singular vectors. Another common, and
entirely equivalent, form of notation for the same quantity that is
often used in the mechanics literature is the dyadic
form 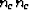 .
.
The elastic potential 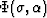 then takes the form
then takes the form
| ![\begin{displaymath}
\begin{array}
{rclclcl}
\Phi(\sigma,\alpha) & = & \Phi^{(0)}...
..._7 [\hbox{Tr}(\sigma\cdot\alpha\cdot\alpha)]^2, & &\end{array} \end{displaymath}](img117.gif) |
(38) |
where 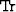 is the trace operation, and the dot notation
indicates a contraction over one set of indices.
(Note that the significance of crack-influence parameters
is the trace operation, and the dot notation
indicates a contraction over one set of indices.
(Note that the significance of crack-influence parameters 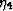 ,
, 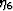 , and
, and
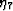 have been changed from the definitions made by Kachanov (1980),
Kachanov and Sevostianov (2005), and Sayers and Kachanov (1991), so that here
have been changed from the definitions made by Kachanov (1980),
Kachanov and Sevostianov (2005), and Sayers and Kachanov (1991), so that here
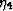 is the coefficient of a contribution second order in
is the coefficient of a contribution second order in  ,
,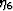 third order in
third order in  , and
, and 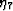 fourth order in
fourth order in  .)
The coefficients pertinent to the isotropic background elastic medium
are given by
.)
The coefficients pertinent to the isotropic background elastic medium
are given by 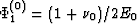 and
and 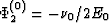 ,where E0 is Young's modulus, and
,where E0 is Young's modulus, and 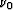 is Poisson's ratio.
is Poisson's ratio.
Now, to illustrate the meaning of (38), we will
reduce this to component form in two cases. For the cases of interest, we
can assume
the crack density tensor itself reduces to the form
| 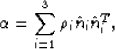 |
(39) |
where 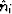 , for i = 1,2,3, correspond to spatial directions
x, y, z, respectively. Furthermore,
, for i = 1,2,3, correspond to spatial directions
x, y, z, respectively. Furthermore, 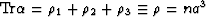 is the scalar crack density
defined in the main text.
is the scalar crack density
defined in the main text.
Horizontal cracks, 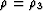
If all the cracks in the system have the same axis of symmetry (which
we will take to be the z-axis), then 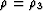 and
(38) reduces to the following expression:
and
(38) reduces to the following expression:
| 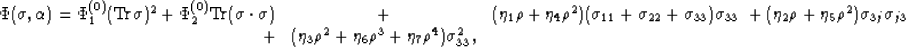 |
(40) |
where the repeated index j is summed. At low crack densities
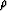 , we see that
only the terms proportional to
, we see that
only the terms proportional to 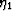 and
and 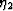 are important in
the crack-influence decomposition. As the crack density increases,
the terms proportional to
are important in
the crack-influence decomposition. As the crack density increases,
the terms proportional to 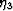 ,
, 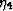 , and
, and 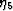 start to
contribute.
Then, at the highest crack densities considered, all seven of these
coefficients can come into play. Although we may imagine for
example that
start to
contribute.
Then, at the highest crack densities considered, all seven of these
coefficients can come into play. Although we may imagine for
example that 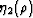 is actually a function of crack density
is actually a function of crack density 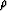 ,it is clear from the form of (40) that such corrections
would be indistinguishable from corrections due to
,it is clear from the form of (40) that such corrections
would be indistinguishable from corrections due to 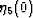 .So, for our present purposes, we do not need to consider any
coefficients except
.So, for our present purposes, we do not need to consider any
coefficients except 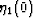 and
and 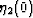 at low crack
densities,
and we also do not need to consider any coefficients except
at low crack
densities,
and we also do not need to consider any coefficients except
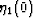 through
through 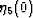 , when we want to fit quadratic
corrections for the moderate crack density results.
, when we want to fit quadratic
corrections for the moderate crack density results.
Typical values of 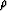 of interest in many applications are around
of interest in many applications are around
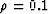 . So as long as the
. So as long as the  's for higher order corrections
are of approximately the same order of magnitude as those for
's for higher order corrections
are of approximately the same order of magnitude as those for
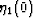 and
and 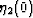 , we see that neglect of terms
like
, we see that neglect of terms
like 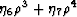 is entirely appropriate.
is entirely appropriate.
Now it is also easy to see how (40) gives rise
to the low density result (4).
Vertical cracks, 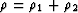
It is also straightforward now to repeat the previous exercise by
considering other types of crack density distribution. An interesting
case is the one with all vertical cracks, having their crack normals
in the xy-plane. Then, 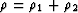 . A special case of
this type is when the crack normals are completely randomly distributed so
that
. A special case of
this type is when the crack normals are completely randomly distributed so
that 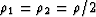 . Then, we get simplified formulas for
all the terms in the elastic potential analogous to the previous
example. The results are:
. Then, we get simplified formulas for
all the terms in the elastic potential analogous to the previous
example. The results are:
| 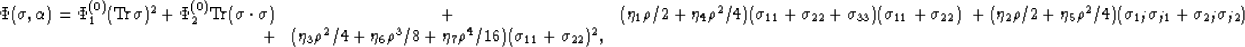 |
(41) |
where again the repeated index j is summed.
The basic conclusions reached in the previous example clearly apply
again. For small to moderate crack densities 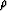 , we do not
need to consider
, we do not
need to consider 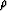 dependence of crack-influence parameters
dependence of crack-influence parameters
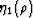 or
or 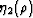 ,as such dependence cannot be distinguished from the low order
contributions from
,as such dependence cannot be distinguished from the low order
contributions from 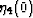 and
and 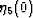 , respectively.
Similarly,
, respectively.
Similarly, 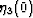 comes into play whenever
comes into play whenever 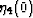 and
and
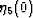 are important, while
are important, while 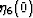 and
and 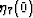 can
presumably be neglected in many low to moderate crack density applications.
can
presumably be neglected in many low to moderate crack density applications.
T
ABLE 2.Examples of Sayers and Kachanov (1991)
crack-influence parameters
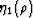
and
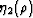
when crack density
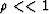
for penny-shaped cracks. Four choices of effective medium theory are
considered: NI (non-inteacting), DS, (differential scheme), CPA
(coherent potential approximation), and SC (the Budiansky and
O'Connell self-consistent scheme). Note that crack density is defined
here as
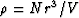
, where
N/
V is number density of cracks,
and
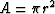
is the area of the circular crack face.
![\begin{displaymath}
0.15in]
\begin{tabular}
{\vert c\vert cc\vert} \hline\hline...
...8 & 0.0290 \
SC & -0.0000207 & 0.0290 \hline\hline\end{tabular}\end{displaymath}](img143.gif)





Next: APPENDIX C. DISCUSSION OF
Up: Berryman and Grechka: Random
Previous: Self-consistent Estimates for Hexagonal
Stanford Exploration Project
1/16/2007
![]() then takes the form
then takes the form
![\begin{displaymath}
\begin{array}
{rclclcl}
\Phi(\sigma,\alpha) & = & \Phi^{(0)}...
..._7 [\hbox{Tr}(\sigma\cdot\alpha\cdot\alpha)]^2, & &\end{array} \end{displaymath}](img117.gif)
![]()
![]() and
(38) reduces to the following expression:
and
(38) reduces to the following expression:
![]() of interest in many applications are around
of interest in many applications are around
![]() . So as long as the
. So as long as the ![]() 's for higher order corrections
are of approximately the same order of magnitude as those for
's for higher order corrections
are of approximately the same order of magnitude as those for
![]() and
and ![]() , we see that neglect of terms
like
, we see that neglect of terms
like ![]() is entirely appropriate.
is entirely appropriate.
![]()
![]() . A special case of
this type is when the crack normals are completely randomly distributed so
that
. A special case of
this type is when the crack normals are completely randomly distributed so
that ![]() . Then, we get simplified formulas for
all the terms in the elastic potential analogous to the previous
example. The results are:
. Then, we get simplified formulas for
all the terms in the elastic potential analogous to the previous
example. The results are:
![]() , we do not
need to consider
, we do not
need to consider ![]() dependence of crack-influence parameters
dependence of crack-influence parameters
![]() or
or ![]() ,as such dependence cannot be distinguished from the low order
contributions from
,as such dependence cannot be distinguished from the low order
contributions from ![]() and
and ![]() , respectively.
Similarly,
, respectively.
Similarly, ![]() comes into play whenever
comes into play whenever ![]() and
and
![]() are important, while
are important, while ![]() and
and ![]() can
presumably be neglected in many low to moderate crack density applications.
can
presumably be neglected in many low to moderate crack density applications.
![\begin{displaymath}
0.15in]
\begin{tabular}
{\vert c\vert cc\vert} \hline\hline...
...8 & 0.0290 \
SC & -0.0000207 & 0.0290 \hline\hline\end{tabular}\end{displaymath}](img143.gif)