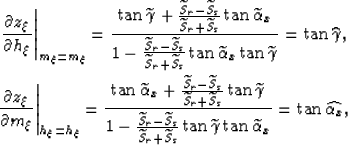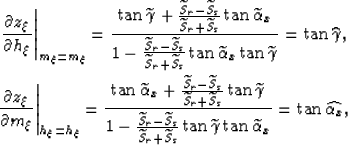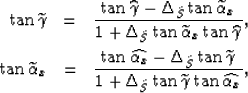Next: Kinematics of the angle-domain
Up: Angle-Domain Common-Image Gathers
Previous: Theory of ADCIGs in
From the ``plane-wave'' viewpoint of the theory of ADCIGs in
anisotropic media, the expression for the generalized impulse response of prestack
anisotriopic migration leads to the following expressions for the
offset and midpoint dips:
| 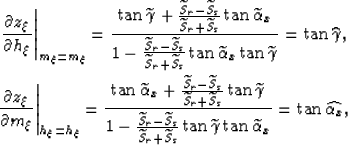 |
(5) |
| (6) |
where 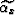 is the group dip angle,
is the group dip angle, 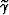 is
the group average aperture angle,
is
the group average aperture angle, 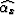 and
and
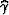 are two angles we introduce and that are related to
the midpoint and offset dips.
are two angles we introduce and that are related to
the midpoint and offset dips. 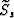 and
and 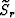 are
the phase slownesses for the source and receiver
wavefields, respectively.
are
the phase slownesses for the source and receiver
wavefields, respectively.
The phase aperture and group dip angles can then be related
to the offset and midpoint image dips:
| 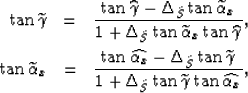 |
(7) |
| (8) |
where 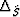 is the ``normalized slowness difference''
is the ``normalized slowness difference''
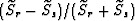 .
.





Next: Kinematics of the angle-domain
Up: Angle-Domain Common-Image Gathers
Previous: Theory of ADCIGs in
Stanford Exploration Project
4/6/2006